��Ŀ����
����Ŀ����ͼ��ʾ���̶�ľ��BC��ˮƽ����B��ƽ�����ӣ�һ�����ˮƽ����A����![]() �ij��ٶ����һ�ȥ����֪�����ˮƽ���Ķ�Ħ������
�ij��ٶ����һ�ȥ����֪�����ˮƽ���Ķ�Ħ������![]() ,��ľ���Ķ�Ħ������
,��ľ���Ķ�Ħ������![]() �������ٶ�
�������ٶ�![]() ,AB��ľ���Ϊs=2 m,ľ������Ϊ
,AB��ľ���Ϊs=2 m,ľ������Ϊ![]() ��ľ���㹻������
��ľ���㹻������
(1)�����ľ���ϻ��еľ���
(2)����A���˶���ľ������ߵ����õ�ʱ�䣻
(3)������������ͳ������ٶȲ��䣬Ҫʹ�����ľ�������ϻ��еľ�����С����ľ������Ӧ����Ϊ���٣�������������ľ�����˶���ʱ��Ϊ������

���𰸡�(1)0.8m(2)0.8s(3)60��, ![]()
����������1�������ľ���ϵĻ��о���ΪL�����ݶ��ܶ������У�
��1mgs+(mgsin��+��2mgcos��)L��![]() mv02
mv02
�������ݽ�ã�L=0.8m
��2�������ˮƽ���ϻ��еļ��ٶȴ�СΪ��a=��1g��
��v02v2��2��1gs
�������˶���B��ʱ���ٶ�Ϊ��v=4m/s
��s=![]() (v0+v)t1
(v0+v)t1
���t1=0.4s
��L=![]() vt2
vt2
��t2=0.4s
��������˶�����ʱ��Ϊ��t=t1+t2=0.8s��
��3���ɣ�1�����ж��ܶ���֪�� 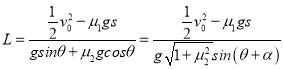
����tan��=��2����=30����
��˵���=60��ʱ��L����СֵL=![]() m
m
�ϻ����ٶ�a1��gsin60��+��2gcos60����![]() m/s2
m/s2
�����˶�����ߵ�ʱ��gsin60������2gcos60��������������б������»������ٶ�Ϊ��
a2��gsin60���2gcos60����![]() m/s2
m/s2
��L=![]() at2�ɵ��ϻ�����ʱ��t3��
at2�ɵ��ϻ�����ʱ��t3��![]() s
s
�»�ʱ��Ϊt4��![]() s��
s��
�����ľ�����˶�����ʱ��Ϊ��t����t3+t4��![]() s��
s��

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�