��Ŀ����
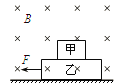
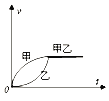
����Ŀ����ͼ��ʾ�����Ϊ37����б�泤L=1.9 m����б������Ϸ���O�㽫һС�����ٶ�v0=3 m/s���ٶ�ˮƽ�׳���ͬʱ��б�涥���ɾ�ֹ�ͷ�һ���飬����һ��ʱ���С��ǡ���ܹ��Դ�ֱб��ķ�����л��顣С��ͻ������Ϊ�ʵ㣬ȡ�������ٶ�g=10 m/s2��sin 37��=0.6��cos 37��=0.8����

��1��С����׳�������б�����õ�ʱ�䣻
��2���׳���O��б��˵ĸ߶ȣ�
��3��������б���Ķ�Ħ����������
���𰸡���1��0.4 s ��2��1.7 m ��3��0.125
�����������������С��ֱ����б�棬����ƽ���ı��ζ��������ֱ���ٶȣ��Ӷ�����˶���ʱ�䣻����С�����ֱλ�ƺ�ˮƽλ�ƣ���ϼ��ι�ϵ����׳��㵽б��˵ĸ߶ȣ�����ţ�ٵڶ����ɣ����λ�ƹ�ʽ��ץסʱ��������������б���Ķ�Ħ��������
��1����С����л���ʱ���ٶ�Ϊv����ֱ���ٶ�Ϊvy
�ɼ��ι�ϵ��tan 370=![]()
��С������ʱ��Ϊt����С�����ֱ���ٶ�vy=gt
�����t=0.4 s
��2����ֱλ��Ϊy��ˮƽλ��Ϊx����ƽ���ɵ��� ![]()
![]()
���׳��㵽б����͵�ľ���Ϊh���ɼ��ι�ϵ��h=y+xtan37��
�����ϸ�ʽ����h=1.7m
��3����ʱ��t�ڣ������λ��Ϊs���ɼ��ι�ϵ���� ![]()
�軬��ļ��ٶ�Ϊa�����˶�ѧ��ʽ�ã� ![]()
�Ի��飬��ţ�ٵڶ����ɵã�mgsin37��-��mgcos37��=ma
�����ϸ�ʽ������=0.125