题目内容
9.设想地球绕太阳公转的圆周轨道半径r,太阳半径Rs和地球半径R三者均减小为现在的1%,而太阳和地球的密度均匀且不变,仅考虑太阳和地球之间的作用力,以现实地球的1年为标准,计算“设想地球”的1年将为1年.分析 地球绕太阳做匀速圆周运动,受到太阳的万有引力,万有引力提供向心力,计算地球的公转周期,太阳的质量等于密度乘以太阳的体积,代入化简,根据表达式和题中数据讨论地球的公转周期的变化.
解答 解:根据万有引力定律,有:$\frac{GMm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$,解得T=$\sqrt{\frac{4{π}^{2}{r}^{3}}{GM}}$,
又因为M=ρV=$ρ•\frac{4}{3}π{{R}_{s}}^{3}$,解得T=$\sqrt{\frac{3π}{Gρ}•\frac{{r}^{3}}{{{R}_{s}}^{3}}}$,
从上式可知,当太阳半径减小为现在的1%时,地球公转周期不变.仍然为1年.
故答案为:1.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,本题的关键得出周期的表达式,从而分析判断.

练习册系列答案
相关题目
19. 如图所示,一圆盘绕一通过圆心O且垂直盘面的竖直轴匀速转动.在圆盘上放置一木块,木块相对圆盘静止随圆盘一起运动,则( )
如图所示,一圆盘绕一通过圆心O且垂直盘面的竖直轴匀速转动.在圆盘上放置一木块,木块相对圆盘静止随圆盘一起运动,则( )
 如图所示,一圆盘绕一通过圆心O且垂直盘面的竖直轴匀速转动.在圆盘上放置一木块,木块相对圆盘静止随圆盘一起运动,则( )
如图所示,一圆盘绕一通过圆心O且垂直盘面的竖直轴匀速转动.在圆盘上放置一木块,木块相对圆盘静止随圆盘一起运动,则( )| A. | 木块受到圆盘对它的摩擦力,方向指向圆心 | |
| B. | 木块受到圆盘对它的摩擦力,方向背离圆心 | |
| C. | 木块受到圆盘对它的摩擦力,方向与木块运动方向相反 | |
| D. | 木块受到圆盘对它的摩擦力,方向与木块运动方向相同 |
17.对声波的各种现象,以下说法中正确的是( )
| A. | 在双缝干涉实验中,把入射光由红色光换成紫色光,相邻亮条纹间距变宽 | |
| B. | 古代某和尚房里挂着的磐常自鸣自响,属于声波的共鸣现象 | |
| C. | 绕正在发音的音叉为圆心走一圈,可以听到忽强忽弱的声音,这是多普勒效应现象 | |
| D. | 把耳朵贴在铁轨上可以听到远处的火车声,属于声波的衍射现象 |
4. 如图所示,与锌板相连的验电器的铝箔原来是张开的,现在让弧光灯发出的光照射到锌板,发现与锌板相连的验电器的铝箔张角变大,此实验事实说明错误的是( )
如图所示,与锌板相连的验电器的铝箔原来是张开的,现在让弧光灯发出的光照射到锌板,发现与锌板相连的验电器的铝箔张角变大,此实验事实说明错误的是( )
 如图所示,与锌板相连的验电器的铝箔原来是张开的,现在让弧光灯发出的光照射到锌板,发现与锌板相连的验电器的铝箔张角变大,此实验事实说明错误的是( )
如图所示,与锌板相连的验电器的铝箔原来是张开的,现在让弧光灯发出的光照射到锌板,发现与锌板相连的验电器的铝箔张角变大,此实验事实说明错误的是( )| A. | 光具有粒子性 | |
| B. | 铝箔张角大小与光照时间无关 | |
| C. | 若改用激光器发出的红光照射锌板,观察到验电器的铝箔张角则一定会变得更大 | |
| D. | 验电器的铝箔原来带正电 |
18.天然放射性元素放出的三种射线的穿透能力实验结果如图所示,由此可知( )


| A. | ②来自于原子核外的电子 | |
| B. | ①的电离作用最强,是一种电磁波 | |
| C. | ③的电离作用最强,是一种电磁波 | |
| D. | ③的电离作用最弱,属于原子核内释放的光子 |
 平行板电容器AB两极板之间电压为U,间距为d.下极板与一个直径为L的半圆形金属通道相连,金属通道有两个同心的半圆形金属片CD组成,圆心贴在O′处,两个金属片彼此靠近又不接触,中间存在径向电场,即电场大小相等,方向都指向O′.半圆形通道与下极板接触点有小孔相连通.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计),粒子在半圆形轨道间运动而不会发生碰撞.
平行板电容器AB两极板之间电压为U,间距为d.下极板与一个直径为L的半圆形金属通道相连,金属通道有两个同心的半圆形金属片CD组成,圆心贴在O′处,两个金属片彼此靠近又不接触,中间存在径向电场,即电场大小相等,方向都指向O′.半圆形通道与下极板接触点有小孔相连通.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m、电荷量为q的带正电微粒(微粒的重力不计),粒子在半圆形轨道间运动而不会发生碰撞. 如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上.当A以O为圆心做半径r=0.2m的匀速圆周运动时,要使B保持不动,求
如图所示,细绳一端系着质量m=0.1kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M=0.5kg的物体B相连,B静止于水平地面上.当A以O为圆心做半径r=0.2m的匀速圆周运动时,要使B保持不动,求 把一根长为L=10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中.
把一根长为L=10cm的直导线垂直磁感线方向放入如图所示的匀强磁场中.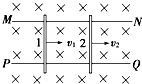 如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )
如图,在水平面上有两条平行导电导轨MN、PQ,导轨间距离为l,匀强磁场垂直于导轨所在的平面(纸面)向里,磁感应强度的大小为B,两根金属杆1、2摆在导轨上,与导轨垂直,它们分别以速度v1、v2做匀速直线运动,下列哪种情形回路中有电流通过 ( )