题目内容
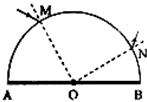一半圆柱形透明物体横截面如图所示，地面AOB镀银，O表示半圆截面的圆心，一束光线在横截面内从M点的入射角为θ，∠MOA为β，且MO⊥ON．求透明物体的折射率．分析：作出光路图，根据几何关系求出光线在M点的折射角．根据折射角，通过折射定律求出透明物体的折射率．
解答：解：如图，
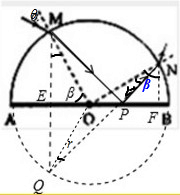
透明物体内部的光路为折线MPN，Q、M点相对于底面EF对称，Q、P和N三点共线
已知在M点处，光的入射角为θ，折射角为r，则∠OMP=∠OQP=r=∠ONP．
又∠ONF=∠MOA=β
由几何知识：∠MQP=∠PNF
即：90°-β+r=β-r
得：2r=90°-2β
则：r=45°-β
根据折射定律：n=
=
答：透明物体的折射率为
．
透明物体内部的光路为折线MPN，Q、M点相对于底面EF对称，Q、P和N三点共线
已知在M点处，光的入射角为θ，折射角为r，则∠OMP=∠OQP=r=∠ONP．
又∠ONF=∠MOA=β
由几何知识：∠MQP=∠PNF
即：90°-β+r=β-r
得：2r=90°-2β
则：r=45°-β
根据折射定律：n=
| sinθ |
| sinr |
| sinθ |
| sin(β-45°) |
答：透明物体的折射率为
| sinθ |
| sin(β-45°) |
点评：本题主要考查光的折射和反射，掌握折射定律，本题对数学几何能力的要求较高．
练习册系列答案
阅读快车系列答案
相关题目
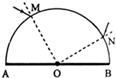一半圆柱形透明物体横截面如图所示，底面AOB镀银（图中粗线），O表示半圆截面的圆心，一束光线在横截面内从M点入射，经过AB面反射后从N点射出．已知光线在M点入射角为30°，∠MOA=60°，∠NOB=30°．求
E．若P点与波源距离s=vT，则质点P的位移与波源的相同
E．若P点与波源距离s=vT，则质点P的位移与波源的相同