题目内容
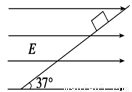
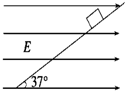 如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止.重力加速度取g,sin 37°=0.6,cos 37°=0.8.
如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止.重力加速度取g,sin 37°=0.6,cos 37°=0.8.求:(1)水平向右的电场的电场强度;
(2)若将电场强度减小为原来的
| 1 | 2 |
分析:(1)对小物块进行受力分析,小物块受重力、斜面支持力和电场力三个力作用,电场力水平向右,根据小物块受力平衡列方程可求电场力的大小,在匀强电场中电场力F=qE,在已知F和q的情况下,可以计算出E.
(2)电场强度减小为原来的
,则小物块受到的电场力减小为原来的
,物块受到的重力不变,支持力方向不变,小物块在垂直于斜面方向所受合力为0,平行于斜面的方向的合力使物块产生加速度.
(2)电场强度减小为原来的
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:
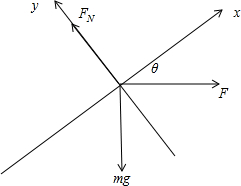
(1)建立如图所示坐标系,对物体进行受力分析,根据平衡列方程:
在x轴方向:F合x=Fcosθ-mgsinθ=0
在y轴方向:F合y=FN-mgcosθ-Fsinθ=0
联列代入θ=37°得:F=
mg
在电场中电场力F=qE可得电场强度E=
=
.
(2)建立如图所示坐标系对物体受力分析有:
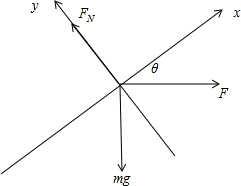
物体在x轴方向所受的合外力为:F合x=Fcosθ-mgsinθ=ma
由此得物体产生的加速度为:a=
又因为电场强度变为原来的
,所以此时物体受到的电场力F=qE′=q
E=q×
×
=
mg
则物体产生的加速度a=
=-0.3g(负号表示方向沿x轴负方向)
所以物体产生的加速度的大小为0.3g.
答:(1)水平向右的电场的电场强度E=
;
(2)若将电场强度减小为原来的
,小物块的加速度是0.3g.

(1)建立如图所示坐标系,对物体进行受力分析,根据平衡列方程:
在x轴方向:F合x=Fcosθ-mgsinθ=0
在y轴方向:F合y=FN-mgcosθ-Fsinθ=0
联列代入θ=37°得:F=
| 3 |
| 4 |
在电场中电场力F=qE可得电场强度E=
| F |
| q |
| 3mg |
| 4q |
(2)建立如图所示坐标系对物体受力分析有:

物体在x轴方向所受的合外力为:F合x=Fcosθ-mgsinθ=ma
由此得物体产生的加速度为:a=
| Fcosθ-mgsinθ |
| m |
又因为电场强度变为原来的
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3mg |
| 4q |
| 3 |
| 8 |
则物体产生的加速度a=
| ||||||
| m |
所以物体产生的加速度的大小为0.3g.
答:(1)水平向右的电场的电场强度E=
| 3mg |
| 4q |
(2)若将电场强度减小为原来的
| 1 |
| 2 |
点评:正确的受力分析,根据平衡列方程可得电场力F的大小,又因电场力F=qE,正确的受力分析并列出方程是解题的关键.

练习册系列答案
相关题目
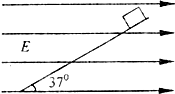 如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止.重力加速度取g,sin37°=0.6,cos37°=0.8.求:
如图所示,一带电荷量为+q、质量为m的小物块处于一倾角为37°的光滑斜面上,当整个装置被置于一水平向右的匀强电场中,小物块恰好静止.重力加速度取g,sin37°=0.6,cos37°=0.8.求: