题目内容
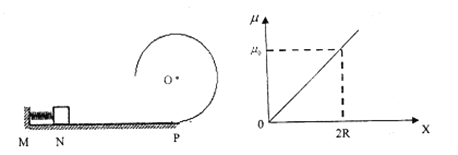
【题目】如图，MP是水平地面，P点是竖直光滑圆形轨道的最低点，半径为R，N、P之间的距离为2R。一个质量为m的小物块（可以看成质点）与竖直墙之间有一个处于压缩状态的轻弹簧，物块与NP之间的动摩擦因数随距N点距离变化的图像如图所示。现把物块从N点由静止释放（重力加速度为g，图像中
已知），求：
（1）若物块达到P点时对轨道的压力为2mg，开始时弹簧的弹性势能为多大；
（2）若物块能滑上圆形轨且在到达圆轨道最高点前不脱离圆形轨道，开始时弹簧的弹性势能大小应满足的条件。
【答案】（1）
（2）
或
【解析】
（1）在P点根据牛顿第二定律有：
由牛顿第三定律：
得：
物块与NP之间的动摩擦因数随距N点距离变化的图像可以看出，全过程的平均动摩擦因数为
，
根据能量守恒：
（2）若恰好到达与圆心登高处：能量守恒：
若恰好到达圆形轨道的最高点：在最高点：
能量守恒：
若物块能滑上圆形轨且在到达圆轨道最高点前不脱离圆形轨道：
或
练习册系列答案
教材全解字词句篇系列答案
相关题目
