题目内容
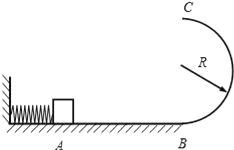
【题目】如图所示，光滑水平面与竖直面的半圆形导轨在B点相连接，导轨半径为R，一个质量为m的静止的木块在A处压缩轻质弹簧，释放后，木块获得向右的初速度，当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的9倍，之后沿半圆导轨向上运动，恰能通过轨道最高点C，不计空气阻力，试求：
（1）弹簧对木块所做的功；
（2）木块从B到C过程中摩擦力所做的功；
（3）木块离开C点落回水平地面时的动能．
【答案】（1）4mgR；（2）
（3）
【解析】试题分析：（1）由B点对导轨的压力可求得物体在B点的速度，则由动能定理可求得弹簧对物块的弹力所做的功；（2）由临界条件利用向心力公式可求得最高点的速度，由动能定理可求得摩擦力所做的功；（3）木块离开C后做平抛运动，机械能守恒，由机械能守恒定律可以求出落地动能．
（1）设木块经过B点进入半圆形导轨瞬间，所受支持力为
，则由牛顿第二定律： 
由题意和牛顿第三定律得： 
可得，木块经过B点的动能： 
由动能定理得：弹簧对木块做的功与B点动能相等，为4mgR
（2）木块恰能通过轨道最高点C，在C点，由牛顿第二定律得： 
木块从B到C过程中，运用动能定理得： 
由上各式可得： 
（3）木块离开C点落回水平地面的过程只有重力做功，故该过程机械能守恒，设地面为零势能面，木块离开C点落回水平地面时的动能： 
练习册系列答案
一线名师提优试卷系列答案
相关题目
