题目内容
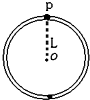 如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )
如图所示,半径为L的圆管轨道(圆管内径远小于轨道半径)竖直放置,管内壁光滑,管内有一个小球(小球直径略小于管内径)可沿管转动,设小球经过最高点P时的速度为v,则( )A、v的最小值为
| ||
| B、v若增大,球所需的向心力也增大 | ||
C、当v由
| ||
D、当v由
|
分析:管子与轻杆模型类似,在最高点能支撑小球,临界速度为零;向心力公式为Fn=m
;小球经过最高点P时,可能是下管壁对小球有支持力,也可能是上管壁对小球有压力,根据牛顿第二定律列式分析轨道对球的弹力.
| v2 |
| r |
解答:解:A、由于在最高点P管子能支撑小球,所以的最小值为零,故A错误.
B、根据向心力公式Fn=m
=m
,可知v增大,球所需的向心力也增大,故B正确.
CD、小球经过最高点P时,当v=
时,根据牛顿第二定律得知:管壁对小球没有作用;
当v由
逐渐减小时,下管壁对小球有支持力,根据牛顿第二定律得:
mg-N=m
,
得:N=mg-m
,v减小,轨道对球的弹力N增大;
当v由
逐渐增大时,根据牛顿第二定律得:
mg+N=m
,
得:N=m
-mg,v增大,轨道对球的弹力N增大;故C错误,D正确.
故选:BD.
B、根据向心力公式Fn=m
| v2 |
| r |
| v2 |
| L |
CD、小球经过最高点P时,当v=
| gL |
当v由
| gL |
mg-N=m
| v2 |
| L |
得:N=mg-m
| v2 |
| L |
当v由
| gL |
mg+N=m
| v2 |
| L |
得:N=m
| v2 |
| L |
故选:BD.
点评:本题要抓住管子与轻杆模型的相似性,知道在最高点,管子对球的弹力可能向下,也可能向上,与球的速度有关,抓住合外力提供向心力这一基本思路进行分析.

练习册系列答案
相关题目
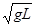
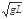
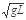 逐渐减小时,轨道对球的弹力也减小
逐渐减小时,轨道对球的弹力也减小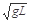 逐渐增大时,轨道对球的弹力也增大
逐渐增大时,轨道对球的弹力也增大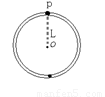
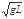
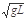 逐渐减小时,轨道对球的弹力也减小
逐渐减小时,轨道对球的弹力也减小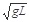 逐渐增大时,轨道对球的弹力也增大
逐渐增大时,轨道对球的弹力也增大