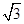题目内容
(17分)如图所示，在倾角为θ的粗糙斜面上，一个质量为m的物体被水平力F推着静止于斜面上，物体与斜面间的动摩擦因数为μ，且μ＜tanθ，求力F的取值范围．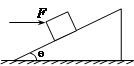
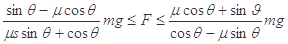
因为μ<tanθ，所以当F=0时，物体不能静止.
若物体在力F的作用下刚好不下滑，则物体受沿斜面向上的最大静摩擦力，且此时F最小，对物体受力分析，如图甲所示，
由平衡条件：
mgsinθ=Fcosθ+f ①
N=mgcosθ+Fsinθ ②
F=μN ③
由①②③得Fmin=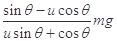
若物体在力F的作用下刚好不上滑，则物体受沿斜面向下的最
大静摩擦力，且此时F最大，对物体受力分析，如图乙所示，
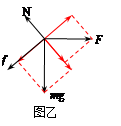
由平衡条件：
mgsinθ+f=Fcosθ ①
N=mgcosθ+Fsinθ ②
F=μN ③
由①②③得Fmax=
故：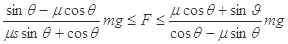
本题考查受力分析的临界问题，物体在力F的作用下刚好不下滑，则物体受沿斜面向上的最大静摩擦力，此时F最小，受力分析后建立直角坐标系，分解后列式求解，物体在力F的作用下刚好不上滑，则物体受沿斜面向下的最大静摩擦力，且此时F最大，同理可求得最大值
若物体在力F的作用下刚好不下滑，则物体受沿斜面向上的最大静摩擦力，且此时F最小，对物体受力分析，如图甲所示，
由平衡条件：
mgsinθ=Fcosθ+f ①
N=mgcosθ+Fsinθ ②
F=μN ③
由①②③得Fmin=
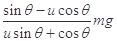
若物体在力F的作用下刚好不上滑，则物体受沿斜面向下的最
大静摩擦力，且此时F最大，对物体受力分析，如图乙所示，
由平衡条件：
mgsinθ+f=Fcosθ ①
N=mgcosθ+Fsinθ ②
F=μN ③
由①②③得Fmax=
故：
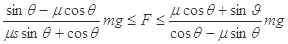
本题考查受力分析的临界问题，物体在力F的作用下刚好不下滑，则物体受沿斜面向上的最大静摩擦力，此时F最小，受力分析后建立直角坐标系，分解后列式求解，物体在力F的作用下刚好不上滑，则物体受沿斜面向下的最大静摩擦力，且此时F最大，同理可求得最大值
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
、m。细杆长度是球面半径的
倍。两球处于平衡状态时，有关下列说法正确的是 
B.
D.
