题目内容
如图所示的竖直平面内有范围足够大、水平向左的匀强电场，在虚线的左侧有垂直纸面向里的匀强磁场，磁感应强度大小为B.一绝缘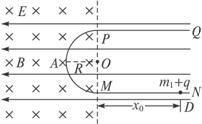
形弯杆由两段直杆和一半径为R的半圆环组成，固定在纸面所在的竖直平面内．PQ、MN水平且足够长，半圆环MAP在磁场边界左侧，P、M点在磁场边界线上，NMAP段是光滑的.现有一质量为m、带电+q的小环套在MN杆上，它所受电场力为重力的
倍.现在M右侧D点由静止释放小环，小环刚好能到达P点. 
(1)求DM间距离x0；
(2)求上述过程中小环第一次通过与O等高的A点时弯杆对小环作用力的大小；
(3)若小环与PQ间动摩擦因数为μ(设最大静摩擦力与滑动摩擦力大小相等),现将小环移至M点右侧4R处由静止开始释放，求小环在整个运动过程中克服摩擦力所做的功．
(1)小环刚好到达P点时速度vP=0
由动能定理得qEx0-2mgR=0 ①
qE=
②
由①②得x0=
.
(2)小环在A点时的速度为va,由动能定理
qE(x0+R)-mgR=
mva2-0 ③
弹力与洛伦兹力合力提供向心力N-qvAB-qE=m
④
由③④得N=
+
.
(3)若-f=μmg≥qE，即μ≥
小环第一次到达P点右侧s1距离处速度为零,由动能定理
qE(4R-s1)-2mgR-fs1=0 ⑤
f=μmg ⑥
由⑤⑥得s1=
环停在此处不动,所以克服摩擦力所做的功W=fs1=
若f-μmg
环经来回往复运动,最后只能在PD之间往复运动,克服摩擦力做功W.
qE(4R)-mg(2R)-W=0
解得W=mgR.
（2011?椒江区模拟）甲、乙、丙三个小球分别位于如图所示的竖直平面内，甲乙在同一条竖直线上，甲丙在同一条水平线上，水平面的P点在丙的正下方，在同一时刻，甲乙丙开始运动，甲以水平速度v0做平抛运动，乙以水平速度v0沿水平面向右做匀速直线运动，丙做自由落体运动，则（ ）
如图所示的竖直平面内有范围足够大、水平向左的匀强电场，电场强度为E．一绝缘弯杆由两段直杆和一半径R=1.6m的四分之一圆弧杆MN组成，固定在竖直面内，两直杆与圆弧杆的连接点分别是M、N，竖直杆PM和水平杆NQ均足够长，PMN段光滑．现有一质量为m1=0.2kg、带电荷量为+q的小环套在PM杆上，从M点的上方的D点静止释放，恰好能达到N点．已知q=2×10-2C，E=2×102N/m．g取10m/s2．
如图所示，甲、乙、丙三小球分别位于如图所示的竖直平面内，甲、乙在同一条竖直直线上，甲、丙在同一条水平线上，P点在丙球正下方．某时刻，甲、乙、丙同时开始运动，甲以水平速度v0平抛，乙以水平速度v0沿水平面向右做匀速直线运动，丙做自由落体运动，则下列说法正确的是（ ）
甲、乙、丙三个小球分别位于如图所示的竖直平面内，甲、丙在同一条水平线上、间距为s，乙、丙在同一条竖直线上、间距为h．三球在同一时刻开始运动，甲以初速度v甲做平抛运动，乙以初速度v乙做竖直上抛运动，丙做自由落体运动，且v乙＞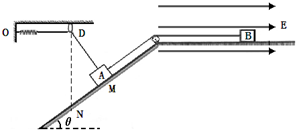
（2013?四川）在如图所示的竖直平面内，物体A和带正电的物体B用跨过定滑轮的绝缘轻绳连接，分别静止于倾角θ=370的光滑斜面上的M点和粗糙绝缘水平面上，轻绳与对应平面平行．劲度系数K=5N/m的轻弹簧一端固定在0点，一端用另一轻绳穿过固定的光滑小环D与A相连，弹簧处于原长，轻绳恰好拉直，DM垂直于斜面．水平面处于场强E=5×104N/C、方向水平向右的匀强电场中．已知A、B的质量分别为mA=0.1kg和mB=0.2kg，B所带电荷量q=+4×l0-6C．设两物体均视为质点，不计滑轮质量和摩擦，绳不可伸长，弹簧始终在弹性限度内，B电量不变．取g=lOm/s2，sin37°=0.6，cos37°=0.8．