Question

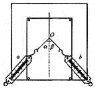
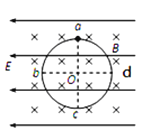
【题目】如图所示，将质量为m的小球用橡皮筋悬挂在竖直墙的O点，小球静止在M点，N为O点正下方一点，ON间的距离等于橡皮筋原长，在N点固定一铁钉，铁钉位于橡皮筋右侧。现对小球施加拉力F，使小球沿以MN为直径的圆弧缓慢向N运动，P为圆弧上的点，角PNM为60°。橡皮筋始终在弹性限度内，不计一切摩擦，重力加速度为g，则下列正确的是（ ）

A. 在P点橡皮筋弹力大小为

B. 在P点时拉力F大小为

C. 小球在M向N运动的过程中拉力F先变大后变小

D. 小球在M向N运动的过程中拉力F的方向始终跟橡皮筋垂直

Answer 1

【答案】ABD

【解析】

设圆的半径为R，橡皮筋的劲度系数为k，角PNM用θ表示，则：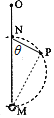

＝2Rcosθ＝2Rcos60°＝R；在M点橡皮筋弹力大小为mg，则：mg=k2R；P点橡皮筋弹力大小为：F0=kR=mg．此时拉力F等于mg与弹簧弹力F0的合力，大小为，故AB正确；结合A的分析可知，当小球与N的连线与竖直方向之间的夹角为α时，橡皮筋的伸长量：△x=2Rcosα；橡皮筋的弹力：F′=k△x=mgcosα；

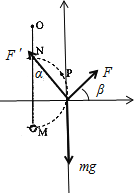
对小球，设拉力F与水平方向之间的夹角为β，在水平方向：Fcosβ=F′sinα；竖直方向：F′cosα+Fsinβ=mg；联立可得：β=α，F=mgsinα；可知拉力F的方向绳子与橡皮筋的方向垂直，而且随α的增大，F逐渐增大。故D正确，C错误；故选ABD。