题目内容
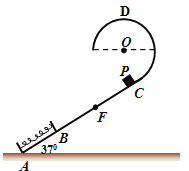
【题目】如图所示,“蜗牛状”轨道OAB竖直固定在水平地面BC上,与地面在B处平滑连接.其中,“蜗牛状”轨道由内壁光滑的两个半圆轨道OA、AB平滑连接而成,半圆轨道OA的半径R=0.6 m,下端O刚好是半圆轨道AB的圆心.水平地面BC长xBC=7 m,C处是一深坑.一质量m=0.5 kg的小球,从O点沿切线方向以某一初速度v0进入轨道OA后,沿OAB轨道运动至水平地面.已知小球与水平地面间的动摩擦因数μ=0.7,取g=10 m/s2.
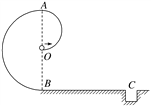
(1)为使小球不脱离OAB轨道,小球在O点的初速度v0的最小值vmin多大?
(2)若v0=9 m/s,求小球在B点对半圆轨道的压力大小;
(3)若v0=9 m/s,通过计算说明小球能否落入深坑?
【答案】(1)6 m/s (2)48.75 N (3)能落入深坑
【解析】试题分析:在A点由向心力公式可求得A点的速度;再对OA过程由动能定理可求得最小速度;对OB过程由动能定理可求得B点的速度,再由向心力公式可求得压力;对物体在水平面上的运动过程分析,由牛顿第二定律及运动学公式可分析小球能否落入深坑。
(1)在A点,由牛顿第二定律得: ![]()
O→A,由动能定理得: ![]()
代入数据得vmin=6 m/s
(2)O→B,由动能定理: ![]()
B点,由牛顿第二定律得: ![]()
代入数据得FN=48.75 N
根据牛顿第三定律,小球在B点对半圆轨道的压力FN′=FN=48.75 N.
(3)在水平面上,设小球从B到停止的过程中经过的位移为x,
由运动学公式-2ax=0-v
由牛顿第二定律μmg=ma
代入数据得x=7.5 m>xBC=7 m
故小球能落入深坑.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目