题目内容
【题目】如图所示,一轻质弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然伸长状态。直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内。质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R。已知P与直轨道间的动摩擦因数μ=0.25,重力加速度大小为g。(取sin370=0.6,cos370=0.8)
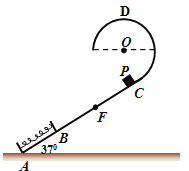
(1)求P第一次运动到B点时速度的大小;
(2)求P运动到E点时弹簧的弹性势能;
(3)改变物块P的质量,将P推至E点,从静止开始释放。P到达圆轨道最高点D时对轨道的压力为重力的0.2倍,求P运动到D点时速度的大小和改变后小物块P的质量。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)选P为研究对象,设运动到B点速度为vB
由动能定理: ![]()
可得: ![]()
(2)P从C点出发,最终静止在F,分析整段过程;
设E点离B点的距离为x,从C点到F全过程
由动能定理: ![]()
可得:![]()
则从C点到E点由能量守恒:
![]()
可得:![]()
(3)在最高点D,由牛顿第二定律可得:![]()
解得:![]()
研究P从E点到D点过程,设P此时质量为m,此过程中:
重力做功为:![]()
摩擦力做功:![]()
弹力做功:![]()
由动能定理:![]()
将⑦⑧⑨⑩代入,可得:![]()

练习册系列答案
相关题目