题目内容
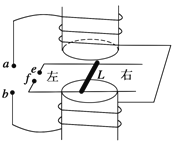
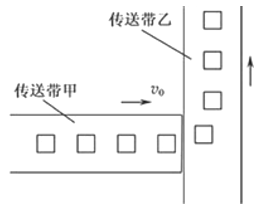
【题目】如图所示,生产车间有两个相互垂直且等高的水平传送带甲和乙,甲的速度为v0，小工件离开甲前与甲的速度相同，并平稳地传到乙上，工件与乙之间的动摩擦因数为μ。乙的宽度足够大，重力加速度为g，则（ ）
A. 若乙的速度为 v0,工件在乙上侧向( 垂直于乙的运动方向)滑过的距离s=
B. 若乙的速度为 2v0,工件从滑上乙到在乙上侧向滑动停止所用的时间不变
C. 若乙的速度为 2v0,工件在乙上刚停止侧向滑动时的速度大小v=
D. 保持乙的速度 2v0 不变,当工件在乙上刚停止滑动时,下一只工件恰好传到乙上,如此反复. 若每个工件的质量均为m,除工件与传送带之间摩擦外,其他能量损耗均不计,驱动乙的电动机的平均输出功率
=
mgμv0
【答案】CD
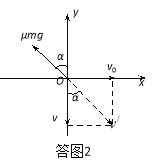
【解析】当乙的速度为v时，工件相对乙的速度与y轴方向的夹角为α
工件受到的摩擦力与二者相对速度的方向相反，如图所示。
A、若乙的速度为v0，甲刚滑上乙时，工件相对乙运动的速度为
， 
工件受到摩擦力的大小为f=μmg， 沿x轴方向，根据牛顿运动定律和运动学公式
，
解得工件在乙上垂直于乙的运动方向滑行的距离
，A错误；
B、若乙的速度为v, 甲刚滑上乙时， 
沿x轴方向，根据牛顿运动定律和运动学公式：
， 
乙的速度不同， 
角不同，工件从滑上乙到在乙上侧向滑动停止所用的时间不同，B错误；
C、工件在乙上停止侧向滑动时与乙相对静止，有相同的速度，v=
，C正确；
D、保持乙的速度 2v0 不变, 甲刚滑上乙时，工件相对乙运动的速度为
，最后与乙相对静止，相对速度为零，受到与相对速度相反的摩擦力，根据牛顿第二定律： 
工件滑动的时间： 
， 
相对滑行的距离： 
， 
此过程产生的内能： 
此过程动能的增量： 
根据能量转化与守恒定律，传送带对工件做功的功率：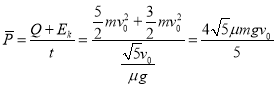 
驱动乙的电动机的平均输出功率
=
mgμv0，D正确。
故选CD。
