题目内容

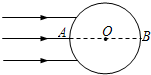精英家教网如图所示是一透明的圆柱体的横截面，其半径为R，折射率为
3
，AB是一条直径，今有一束平行光沿AB方向射向圆柱体，试求距离AB直线多远的入射光线，折射后恰经过B点．
分析：作出光路图，由几何知识分析得到，入射角等于折射角的2倍，由折射定律求出入射角．由数学知识求解入射光线距离AB的距离．
解答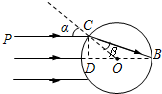：精英家教网（解：设光线P经折射后经过B点，光路图如图所示．
由折射定律有：
sinα
sinβ
=n=
3
  …①
又由几何关系有：α=2β…②
联解①②得α=60°                
由几何关系得：离AB直线的距离CD=Rsinα=
3
2
R的光线经折射后能到达B点．
答：离AB直线的距离CD=Rsinα=
3
2
R的光线经折射后能到达B点．
点评：本题是折射定律的应用，关键是画出光路图，运用几何知识求解入射角与折射角，即可求解．
练习册系列答案
相关题目
如图所示是某公司设计的“2009”玩具轨道，是用透明的薄壁圆管弯成的竖直轨道，其中引入管道AB及“200”管道是粗糙的，AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
1
4
圆管轨道，已知AB圆管轨道半径与“0”字型圆形轨道半径相同．“9”管道是由半径为2R的光滑
1
4
圆弧和半径为R的光滑
3
4
圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成，“200”管道和“9”管道两者间有一小缝隙P，现让质量m=0.5kg的闪光小球（可视为质点）从距A点高H=2.4m处自由下落，并由A点进入轨道AB，已知小球到达缝隙P时的速率为v=8m/s，g取10m/s2．求：
（1）小球通过粗糙管道过程中克服摩擦阻力做的功；
（2）小球通过“9”管道的最高点N时对轨道的作用力；
（3）小球从C点离开“9”管道之后做平抛运动的水平位移以及小球落地时速度的大小．
一个半径为R的透明圆柱，其横截面积如图所示，该透明圆柱的折射率为
3
，AB是圆的一条直径．现有一平行光沿AB方向射入圆柱体．其中一条光线经过一次折射后恰好经过B点，问：这条入射光线到AB的距离是多少？
由透明介质制成的厚壁容器，其横截面为圆环形，介质的折射率n=
2
，内径r=6cm，外径是内径的
3
倍，如图所示．一细束光沿AB方向射人容器，入射角θ1=45°，光在空气中的传播速率约取3×108m/s，求这束光从射入到第一次射出透明介质所用的时间是
5.7×10-10m/s
5.7×10-10m/s
．
（1）一列简谐波沿波的传播方向先后有相距6m的A、B两点，A靠近波源，且A、B间距离小于该波3倍波长．当A点位移达到正向最大时，B点的位移恰好为零，且向正向运动．经0.5s（小于该波的4倍周期）后，A点位移恰好为零，且沿正向运动，而B点的位移恰好达到负的最大．则这列波的波速：（　　）
A．最小值是3m/s．        B．最小值是4m/s．
C．最大值是36m/s．       D．最大值是204m/s．
（2）由透明介质制成的厚壁容器，其横截面为圆环形，介质的折射率n=
2
，内径r=6cm，外径是内径的
3
倍，如图所示．一细束光沿AB方向射人容器，入射角θ1=45°，光在空气中的传播速率约取3×108m/s，求这束光从射入到第一次射出透明介质所用的时间．
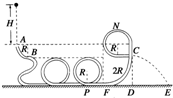精英家教网如图所示是某公司设计的“2009”玩具轨道，是用透明的薄壁圆管弯成的竖直轨道，其中引入管道AB及“200”管道是粗糙的，AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
1
4
圆管轨道，已知AB圆管轨道半径与“0”字型圆形轨道半径相同．“9”管道是由半径为2R的光滑
1
4
圆弧和半径为R的光滑
3
4
圆弧以及两段光滑的水平管道、一段光滑的竖直管道组成，“200”管道和“9”管道两者间有一小缝隙P．现让质量m=0.5kg的闪光小球（可视为质点）从距A点高H=2.4m处自由下落，并由A点进入轨道AB，已知小球到达缝隙P时的速率为v=8m/s，g取10m/s2．求：
（1）小球通过粗糙管道过程中克服摩擦阻力做的功；
（2）小球通过“9”管道的最高点N时对轨道的作用力．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网