题目内容
【题目】A、B两物块(可视为质点)相互挨着放在水平地板上,A与轻弹簧连接,弹簧的另一端固定在墙上,弹簧水平且自然松弛,两物块质量均为1kg,A与地板的摩擦可忽略,B与地板的摩擦因数μ=0.4,现用水平力F推物块B,使A、B将弹簧缓慢压缩x1=10cm,其间力F做功1.4J.
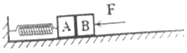
(1)此时弹簧的弹性势能多大;
(2)撤去力F,已知弹簧劲度系数k=200N/m,试求A、B分离时弹簧的形变量x2;
(3)已知弹簧的弹性势能与其形变量的平方成正比,试求A、B分离后,物块B的滑行距离S.
【答案】(1)1J;(2)2cm;(3)6.5cm.
【解析】(1)物体B与地面间的摩擦力为:f=0.4mg=0.4×1×10=4N,
对A、B弹簧系统,根据功能关系,有:WF﹣fx1=Ep弹,
代入数据解得:Ep弹=1J;
(2)A、B分离时刻,A、B间的弹力为零,对B,有:0.4mg=ma,
对A,有:kx2=ma,
联立解得:x2=0.02m=2cm,
此时B的加速度向左,故A的加速度也向左,说明弹簧是伸长的2cm;
(3)已知弹簧的弹性势能与其形变量的平方成正比,令Ep=cx2,最大压缩量为0.1m,此时弹性势能为1J,代入解得:C=400N/m
对从撤去推力到A、B分开瞬间过程,根据功能关系,有: ![]()
解得:v=![]() m/s
m/s
此后A、B分开,B继续滑动,根据动能定理,有:﹣0.4mgs=0﹣![]() mv2
mv2
解得:s=0.065m=6.5cm;

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目