题目内容
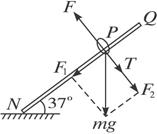
一根光滑绝缘的细杆MN处于竖直面内，与水平面夹角为37°．一个范围较大的水平方向的匀强磁场与细杆相垂直，磁感应强度为B．质量为m的带电小环沿细杆下滑到图中的P处时，向左上方拉细杆的力大小为0.4mg，已知小环的电荷量为q．问：（1）小环带的是什么电？
（2）小环滑到P处时速度有多大？
（3）在离P点多远处，小环与细杆之间没有挤压？
分析：（1）将小球由静止开始释放，小球受到重力、垂直于杆向上的洛伦兹力和杆的垂直于向下的支持力．由左手定则可判定小环的电性．
（2）对小环进行受力分析，垂直于杆的方向上，洛伦兹力大小等于杆的垂直于向下的支持力与重力垂直于杆方向的分力；写出方程，即可求得小环的速度．
（3）分析小球的受力情况和运动情况，由受力分析可知，当洛伦兹力F=mgcos37°时，环与杆之间无挤压．
（2）对小环进行受力分析，垂直于杆的方向上，洛伦兹力大小等于杆的垂直于向下的支持力与重力垂直于杆方向的分力；写出方程，即可求得小环的速度．
（3）分析小球的受力情况和运动情况，由受力分析可知，当洛伦兹力F=mgcos37°时，环与杆之间无挤压．
解答：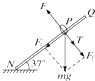
解：
（1）小环下滑时所受的洛伦兹力总是垂直于细杆方向的，只有垂直杆向上才可能使小环向左上方拉杆，由左手定则可判定小环带负电．
（2）小环运动到P处时，受重力mg、洛伦兹力F、杆的弹力T，如图所示．在垂直于杆的方向上，小环受重力的分力F2、杆的拉力T和洛伦兹力F互相平衡：F=T+F2
即：Bqυ=T+mgcos37°
代入数据解得环滑到P点的速度为：υ=
（3）由受力分析可知，当洛伦兹力F=mgcos37°时，环与杆之间无挤压，设此时环的速度为υ′，则：Bqυ′=0.8mg
υ′=
因为υ′＜υ，易知这个位置在P上边某点Q处．令QP=s，因本题中洛伦兹力的变化没有影响小环沿光滑杆下滑的匀加速运动的性质，故有：
υ2=（υ′）2+2as，
即（
）2-（
）2=2gs?sin37°
所以s=
答：（1）小环带的是负电；
（2）小环滑到P处时速度为
；
（3）在离P点
远处，小环与细杆之间没有挤压．
解：（1）小环下滑时所受的洛伦兹力总是垂直于细杆方向的，只有垂直杆向上才可能使小环向左上方拉杆，由左手定则可判定小环带负电．
（2）小环运动到P处时，受重力mg、洛伦兹力F、杆的弹力T，如图所示．在垂直于杆的方向上，小环受重力的分力F2、杆的拉力T和洛伦兹力F互相平衡：F=T+F2
即：Bqυ=T+mgcos37°
代入数据解得环滑到P点的速度为：υ=
| 1.2mg |
| qB |
（3）由受力分析可知，当洛伦兹力F=mgcos37°时，环与杆之间无挤压，设此时环的速度为υ′，则：Bqυ′=0.8mg
υ′=
| 0.8mg |
| qB |
因为υ′＜υ，易知这个位置在P上边某点Q处．令QP=s，因本题中洛伦兹力的变化没有影响小环沿光滑杆下滑的匀加速运动的性质，故有：
υ2=（υ′）2+2as，
即（
| 1.2mg |
| qB |
| 0.8mg |
| qB |
所以s=
| 2m2g |
| 3q2B2 |
答：（1）小环带的是负电；
（2）小环滑到P处时速度为
| 1.2mg |
| qB |
（3）在离P点
| 2m2g |
| 3q2B2 |
点评：本题关键是分析小球的受力情况，判断其运动情况，注意先分析重力和洛伦兹力，抓住洛伦兹力的大小与速度大小成正比进行动态分析．
练习册系列答案
相关题目
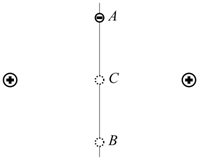（2011?浙江模拟）如图所示，竖直放置一根光滑绝缘细直杆，在其两侧对称固定放置有两个等电荷量的正电荷．细杆上有A、B、C三点，其中C在两电荷的连线和细杆的交点位置，AC=CB=h．一个带负电、质量为m的小球串在细杆上，从A点静止释放运动到B点，则下列说法正确的是（ ）
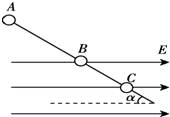如图所示，一根光滑绝缘细杆与水平面成α=30°的角倾斜固定．细杆的一部分处在场强方向水平向右的匀强电场中，场强E=2×104N/C．在细杆上套有一个带电荷量为q=-1.73×10-5C、质量为m=3×10-2kg的小球．现使小球从细杆的顶端A由静止开始沿杆滑下，并从B点进入电场，小球在电场中滑至最远处的C点．已知A、B间的距离x1=0.4m，g=10m/s2．求：
