题目内容
19.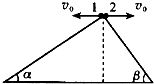 两高度相同的斜面,倾角分别为α、γ,小球1、2分别由斜面顶端以相同水平速度v0抛出,如图所示,假设两球能落在斜面上,则两球的
两高度相同的斜面,倾角分别为α、γ,小球1、2分别由斜面顶端以相同水平速度v0抛出,如图所示,假设两球能落在斜面上,则两球的(1)飞行时间之比tanα:tanβ;
(2)水平位移之比tanα:tanβ;
(3)竖直下落高度之比tan2α:tan2β..
分析 根据竖直位移和水平位移的关系求出飞行时间的表达式,从而得出飞行时间之比.
根据初速度和时间求出水平位移,结合位移时间公式求出竖直下落的高度,从而得出水平位移之比、竖直下落的高度之比.
解答 解:(1)根据tanα=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}=\frac{gt}{2{v}_{0}}$,解得t=$\frac{2{v}_{0}tanα}{g}$,
所以飞行时间之比t1:t2=tanα:tanβ.
(2)水平位移x=v0t,初速度相等,则水平位移之比x1:x2=t1:t2=tanα:tanβ.
(3)竖直下落的高度h=$\frac{1}{2}g{t}^{2}$,则竖直位移之比${h}_{1}:{h}_{2}={{t}_{1}}^{2}:{{t}_{2}}^{2}=ta{n}^{2}α:ta{n}^{2}β$.
故答案为:(1)tanα:tanβ,(2)tanα:tanβ,(3)tan2α:tan2β.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合水平位移和竖直位移的关系求出时间是关键.

练习册系列答案
相关题目
9. 2011年3月11日,日本东北地区发生里氏9.0级大地震,并引发海啸.某网站发布了日本地震前后的卫星图片,据了解该组图片是由两颗卫星拍摄得到的.这两颗卫星均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗卫星分别位于轨道上空的A、B两位置,两卫星与地心的连线间的夹角为60°,如图所示.若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断不正确的是( )
2011年3月11日,日本东北地区发生里氏9.0级大地震,并引发海啸.某网站发布了日本地震前后的卫星图片,据了解该组图片是由两颗卫星拍摄得到的.这两颗卫星均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗卫星分别位于轨道上空的A、B两位置,两卫星与地心的连线间的夹角为60°,如图所示.若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断不正确的是( )
 2011年3月11日,日本东北地区发生里氏9.0级大地震,并引发海啸.某网站发布了日本地震前后的卫星图片,据了解该组图片是由两颗卫星拍摄得到的.这两颗卫星均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗卫星分别位于轨道上空的A、B两位置,两卫星与地心的连线间的夹角为60°,如图所示.若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断不正确的是( )
2011年3月11日,日本东北地区发生里氏9.0级大地震,并引发海啸.某网站发布了日本地震前后的卫星图片,据了解该组图片是由两颗卫星拍摄得到的.这两颗卫星均绕地心O做匀速圆周运动,轨道半径均为r,某时刻两颗卫星分别位于轨道上空的A、B两位置,两卫星与地心的连线间的夹角为60°,如图所示.若卫星均沿顺时针方向运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.下列判断不正确的是( )| A. | 卫星1由位置A运动到位置B的过程中,它所受的万有引力做功不为零 | |
| B. | 卫星2向后喷气就无法追上卫星1 | |
| C. | 这两颗卫星的加速度大小均为$\frac{{R}^{2}g}{{r}^{2}}$ | |
| D. | 卫星1由位置A第一次运动到位置B所用的时间为$\frac{πr}{3R}$$\sqrt{\frac{r}{g}}$ |
14.2008年9月25日至28日,我国成功实施了“神舟”七号载人航天飞行并实现了航天员首次出舱.飞船先沿椭圆轨道飞行,后在远地点343千米处点火加速,由椭圆轨道变成高度为343千米的圆轨道,在此圆轨道上飞船运行周期约为90分钟.下列判断正确的是( )
| A. | 飞船变轨前通过椭圆轨道远地点时的加速度小于变轨后沿圆轨道运动的加速度 | |
| B. | 飞船变轨前通过椭圆轨道远地点时的速度小于变轨后沿圆轨道运动的速度 | |
| C. | 飞船在此圆轨道上运动的角度速度大于同步卫星运动的角速度 | |
| D. | 飞船在圆轨道上时航天员出舱前后都处于失重状态 |
4.如图所示,当磁感应强度B增加时,由内外两金属环组成的月牙形的闭合回路中感应电流方向为( )
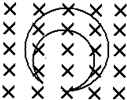

| A. | 内环顺时针,外环逆时针 | B. | 内环逆时针,外环顺时针 | ||
| C. | 内外环均逆时针 | D. | 内外环均顺时针 |
8.将一个小球以初速度v水平抛出,要使小球能够垂直打到一个与水平方向倾角为α的斜面上,那么下列说法正确的是( )
| A. | 若保持水平速度v不变,斜面与水平方向的倾角α越大,小球的飞行时间越长 | |
| B. | 若保持水平速度v不变,斜面与水平方向的倾角α越大,小球的飞行时间越短 | |
| C. | 若保持斜面与水平方向的倾角α不变,水平速度v越大,小球的飞行时间越长 | |
| D. | 若保持斜面与水平方向的倾角α不变,水平速度v越大,小球的飞行时间越短 |
9.关于圆周运动,以下说法正确的是( )
| A. | 匀速圆周运动是匀速运动 | |
| B. | 匀速圆周运动是变速曲线运动 | |
| C. | 向心加速度是描述线速度方向变化的快慢的物理量 | |
| D. | 匀速圆周运动的线速度V是恒量,v方向时刻改变 |
 电动车以其轻便、实用、环保的优点,深受人们的喜爱.如图所示的这辆电动车自重为600N,时速最高可达30km/h,每个车轮与地面的接触面积为100cm2,车胎能承受的最大压强为2×105Pa.
电动车以其轻便、实用、环保的优点,深受人们的喜爱.如图所示的这辆电动车自重为600N,时速最高可达30km/h,每个车轮与地面的接触面积为100cm2,车胎能承受的最大压强为2×105Pa.