��Ŀ����
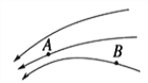
����Ŀ����ͼ��ʾ����һˮƽ���泤L���������˿���С�����֣������������������������������������һ�γ���δ֪�Ĵֲ��棬�������ֹ⻬��С��飨����Ϊ�ʵ㣩���ٶ�![]() ���������������������߷����룬С�����ֲ���Ķ�Ħ��ϵ��
���������������������߷����룬С�����ֲ���Ķ�Ħ��ϵ��![]() ��С���廬������ƽ���˶���������ظ߶�h�Լ�ˮƽ���о���s��Ϊ
��С���廬������ƽ���˶���������ظ߶�h�Լ�ˮƽ���о���s��Ϊ![]() ���������ٶ�Ϊg����
���������ٶ�Ϊg����
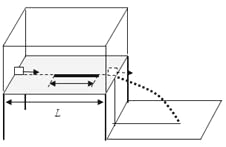
��:��1��δ֪�ֲ���ij���̫Ϊ����?
��2�������С���ӱ������浽��ؾ�����ʱ��Ϊ![]() ����ֲ����ǰ������������˵ľ���?
����ֲ����ǰ������������˵ľ���?
���𰸡���1��![]() ��2��
��2��![]()
�������������������1��ƽ���˶��� ![]()
![]()
ţ�ٵڶ����ɣ� ![]()
ˮƽ����ֱ���˶��� ![]()
�����ö��ܶ����� ![]() ��
��
��ã� ![]()
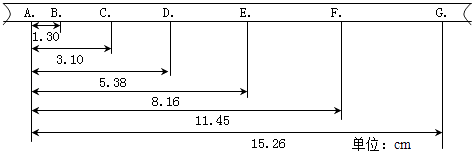
��2����ֲ����ǰ������������˾���Ϊd,��֪![]() ���Ҳ��ֲܴ�����ģ�ĩ�ٶȲ���Ϊ
���Ҳ��ֲܴ�����ģ�ĩ�ٶȲ���Ϊ![]() ��������ʱ�䲻ͬ��
��������ʱ�䲻ͬ��
����ֱ���˶�![]()
�ȼ���ֱ���˶�![]()
����ֱ���˶�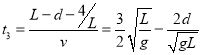
ƽ���˶��� ![]()
��![]() ,��ã�
,��ã� ![]()

��ϰ��ϵ�д�
�����Ŀ