在真空中.半径的圆形区域内有匀强磁场.方向如图所示.磁感应强度B= 0.2 T.一个带正电的粒子以初速度从磁场边界上直径ab的一端a射入磁场.已知该粒子的比荷.不计粒子重力．(1)求粒子在磁场中做匀速圆周运动的半径,(2)若要使粒子飞离磁场时有最大偏转角.求入射时与ab的夹角及粒子的最大偏转角．题目和参考答案——青夏教育精英家教网——

题目内容

（8分）在真空中，半径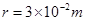的圆形区域内有匀强磁场，方向如图所示，磁感应强度B="0.2" T，一个带正电的粒子以初速度从磁场边界上直径ab的一端a射入磁场，已知该粒子的比荷，不计粒子重力．

（1）求粒子在磁场中做匀速圆周运动的半径；
（2）若要使粒子飞离磁场时有最大偏转角，求入射时与ab的夹角及粒子的最大偏转角．

（1）（2）最大偏转角

解析试题分析：（1）粒子射入磁场后，由于不计重力，所以洛伦兹力提供圆周运动需要的向心力，根据牛顿第二定律有．

（2）粒子在圆形磁场区域运动轨迹为一段半径R=5cm的圆弧，半径一定要使偏转角最大，就要求这段圆弧对应的弦最长，即为图形区域的直径，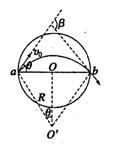

粒子运动轨迹的圆心在ab弦的中垂线上，如图所示．由几何关系可知

最大偏转角
考点：带电粒子在圆形匀强磁场区域的运动

练习册系列答案

精考卷全程测试系列答案

名师点津系列答案

零失误分层训练系列答案

黄冈密卷系列答案

自主创新课时作业系列答案

世纪金榜金榜小博士系列答案

培优竞赛超级课堂系列答案

黄冈小状元达标卷系列答案

黄冈冠军课课练系列答案

高效精练系列答案

相关题目

（9分）如图所示，匀强磁场宽L=30cm，B=3.34×10^-3 T，方向垂直纸面向里，设一质子以v₀=1.6×10⁵ m/s的速度垂直于磁场B的方向从小孔C射入磁场，然后打到照相底片上的A点，质子的质量为1.67×10^-27 kg；质子的电量为1.6×10^-19 C．求：

（1）质子在磁场中运动的轨道半径r；
（2）A点距入射线方向上的O点的距离H；
（3）质子从C孔射入到A点所需的时间t．（，结果保留1位有效数字）

（10分）载流长直导线周围磁场的磁感应强度大小为B＝kI/r，式中常量k>0，I为电流强度，r为距导线的距离。在水平长直导线MN正下方，矩形线圈abcd通以逆时针方向的恒定电流，被两根等长的轻质绝缘细线静止地悬挂，如图所示。开始时MN内不通电流，此时两细线内的张力均为T₀。当MN通以强度为I₁的电流时，两细线内的张力均减小为T₁；当MN内的电流强度变为I₂时，两细线的张力均大于T₀。

(1)分别指出强度为I₁、I₂的电流的方向；
(2)求MN分别通以强度为I₁和I₂电流时，线框受到的安培力F₁与F₂大小之比；
(3)当MN内的电流强度为I₃时两细线恰好断裂，在此瞬间线圈的加速度大小为a，求I₃。

（16分）1932年，劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子，质量为m、电荷量为+q ，在加速器中被加速，加速电压为U。加速过程中不考虑相对论效应和重力作用。

（1）求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；
（2）求粒子从静止开始加速到出口处所需的时间t ；
（3）实际使用中，磁感应强度和加速电场频率都有最大值的限制。若某一加速器磁感应强度和加速电场频率的最大值分别为B_m、f_m，试讨论粒子能获得的最大动能E_㎞。

如图所示，一带正电的质子以速度v₀从O点垂直射入，两个板间存在垂直纸面向里的匀强磁场．已知两板之间距离为d，板长为d，O点是板的正中间，为使粒子能从两板间射出，试求磁感应强度B应满足的条件（已知质子的带电荷量为e，质量为m）

（13分）在一广阔的匀强磁场中，建立一直角坐标系，如图所示，在坐标系的原点O释放一速率为v，质量为m电荷量为十q的粒子（重力不计），释放时速度方向垂直于B的方向，且与x轴成30°角，

则(1)其第一次经过y轴时，轨迹与y轴交点离O点距离为多少？（不考虑空气阻力）
（2粒子从O点开始运动到穿过y轴时所用的时间
（3粒子做圆周运动圆心的坐标

(16分)如图所示的直角坐标系第、象限内存在方向向里的匀强磁场，磁感应强度大小B=0.5T，处于坐标原点O的放射源不断地放射出比荷C/kg的正离子，不计离子之间的相互作用。

⑴求离子在匀强磁场中运动周期；
⑵若某时刻一群离子自原点O以不同速率沿x轴正方向射出，求经过s时间这些离子所在位置构成的曲线方程；
⑶若离子自原点O以相同的速率v₀=2.0×10⁶m/s沿不同方向射入第象限，要求这些离子穿过磁场区域后都能平行于y轴并指向y轴正方向运动，则题干中的匀强磁场区域应怎样调整（画图说明即可）？并求出调整后磁场区域的最小面积。

如图所示，一个质量为m，电荷量为q的带负电的粒子(重力不计)，以初速度v由狭缝S₁，垂直进入电场强度为E的匀强电场中．
(1)为了使此粒子不改变方向从狭缝S₂穿出，则必须在匀强电场区域加入匀强磁场，求匀强磁场B₁的大小和方向．
(2)带电粒子从S₂穿出后垂直边界进入一个矩形区域，该区域存在垂直纸面向里的匀强磁场，粒子运动轨迹如图所示，若射入点与射出点间的距离为L，求该区域的磁感应强度B₂的大小．

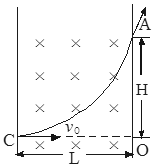
如图所示，用同种电阻丝制成的正方形闭合线框1的边长与圆形闭合线框2的直径相等．m和n是1线框下边的两个端点，p和q是2线框水平直径的两个端点.1和2线框同时由静止开始释放并进入上边界水平、足够大的匀强磁场中，进入过程中m、n和p、q连线始终保持水平．当两线框完全进入磁场以后，下面说法正确的是

A．m、n和p、q电势的关系一定有U_m<U_n，U_p<U_q

B．m、n和p、q间电势差的关系一定有U_mn＝U_pq

C．进入磁场过程中流过1和2线框的电荷量Q₁>Q₂

D．进入磁场过程中流过1和2线框的电荷量Q₁＝Q₂