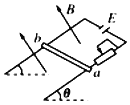
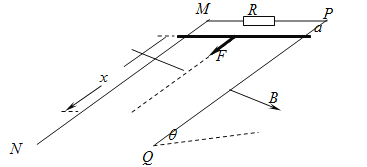
[题目]如图所示.两根足够长的光滑直金属导轨MN.PQ平行固定在倾角θ=37°的绝缘斜面上.两导轨间距L=1m.导轨的电阻可忽略.M.P两点间接有阻值为R的电阻.一根质量m=1kg.电阻r=0.2Ω的均匀直金属杆ab放在两导轨上.与导轨垂直且接触良好．整套装置处于磁感应强度B=0.5T的匀强磁场中.磁场方向垂直斜面向下．自图示位置起.杆ab受到题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，两根足够长的光滑直金属导轨MN、PQ平行固定在倾角θ=37°的绝缘斜面上，两导轨间距L=1m，导轨的电阻可忽略，M、P两点间接有阻值为R的电阻。一根质量m=1kg、电阻r=0.2Ω的均匀直金属杆ab放在两导轨上，与导轨垂直且接触良好．整套装置处于磁感应强度B=0.5T的匀强磁场中，磁场方向垂直斜面向下．自图示位置起，杆ab受到大小为F=0.5v+2（式中v为杆ab运动的速度，力F的单位为N）、方向平行导轨沿斜面向下的拉力作用，由静止开始运动，测得通过电阻R的电流随时间均匀增大．g取10m/s2，sin37°=0.6．

（1）求电阻的阻值R；

（2）金属杆ab自静止开始下滑，通过位移x=1m时电阻R产生的焦耳热Q1=0.8J，求所需的时间t和该过程中拉力F做的功WF。

【答案】（1）0.3Ω（2）

【解析】（1）由题意可知①、

②、

③，

对杆，根据牛顿第二定律有：④

联立①②③④且将F=0.5v+2代入可得⑤

因a与v无关，所以⑥，

R=0.3Ω

（2）由⑤⑥可知⑦

由杆做匀加速直线运动有：⑧，v=at⑨

设电路产生的总热量为Q，则，(10)

由能量转化和守恒， (11)

其中 (12)

由⑦⑧可得t=0.5s，由⑦⑧⑨(10)(11)(12)可得

练习册系列答案

A. 极板M比极板N电势高

B. 加速电场的电压U=ER

C. 直径

D. 若一群离子从静止开始经过上述过程都落在胶片上同一点，则该群离子具有相同的比荷

【题目】如图所示为匀强电场的电场强度E随时间t变化的图象．当t＝0时，在此匀强电场中由静止释放一个带电粒子，设带电粒子只受电场力的作用，则下列说法中正确的是(　　)

A. 带电粒子将始终向同一个方向运动

B. 2 s末带电粒子回到原出发点

C. 3 s末带电粒子的速度为零

D. 0～3 s内，电场力做的总功为零

【题目】如图所示的平面直角坐标系xOy，在第I象限内有平行于x轴的匀强电场，方向沿+x轴方向，在第II象限的三角形PQM区域（含边界）内有匀强磁场，磁感应强度大小为B，方向垂直xOy平面向里。一个带负电的粒子总是从P点沿+y轴方向射入磁场。已知P点坐标为（-L,0），Q点坐标为（-L，L），M点坐标为（0，L），粒子质量为m，电荷量为-q，不计粒子重力。

（1）若粒子从P点射入的速度大小为qLB/m，求粒子从P点射入到刚离开磁场这段时间内平均速度的大小和方向。

（2）若粒子从P点射入后，最终能从x轴上的P、O点间射出，这粒子从P点射入的最大速度为多少？

【题目】用绝缘细线悬挂一个质量为m、带电荷量为+q的小球，让它处于如图所示的磁感应强度为B的匀强磁场中。由于磁场运动，小球静止在如图所示位置，这时悬线与竖直方向夹角为α，并被拉直，则磁场的运动速度和方向是

A. v=，水平向右 B. v=，竖直向上

C. v=，竖直向上 D. v=，竖直向下

【题目】如图甲所示，在直角坐标系区域内有沿y轴正方向的匀强电场，右侧有一个以点（3L，0）为圆心，半径为L的圆形区域，圆形区域与x轴的交点分别为M、N，现有一质量为m，带电量为e的电子，从y轴上的A点以速度沿x轴正方向射入电场，飞出电场后从M点进入圆形区域，速度方向与x轴夹角为30°，此时在圆形区域加如图乙所示周期性变化的磁场，以垂直于纸面向外为磁场正方向，最后电子运动一段时间后从N飞出，速度方向与进入磁场时的速度方向相同（与x轴夹角也为30°），（不考虑磁场变化产生的其他影响），求：

（1）电子进入圆形区域时的速度大小；

（2）区域内匀强电场强度E的大小；

（3）写出圆心磁场区域磁感应强度的大小，磁场变化周期T各应满足的表达式。

【题目】如图，两根间距为d的平行光滑金属导轨间接有电源E，导轨平面与水平面间的夹角θ=30°，金属杆ab垂直导轨放置，导轨与金属杆接触良好，整个装置处于磁感应强度为B的匀强磁场中。当磁场方向垂直导轨平面向上时，金属杆ab刚好处于静止状态。要使金属杆能沿导轨向上运动，可以采取的措施是

A. 将电源正负极对调使金属杆中的电流方向改变

B. 调节滑动变阻器使电阻增大

C. 增大导轨平面与水平面间的夹角θ

D. 增大磁感应强度B

【题目】用如图装置探究产生感应电流的条件实验中，请将相应的实验现象及结论补充完整___________。

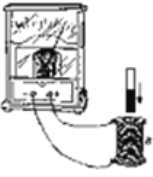
操作方法	电流表的指针
条形磁铁插入线圈过程
(2)条形磁铁插入线圈后静止
(3)条形磁铁取出线圈过程

(4)由以上现象可知：感应电流产生的条件是通过闭合回路的 ___________发生变化。

【题目】如图所示，一根轻弹簧左端固定于竖直墙上，右端被质量为m=1kg可视为质点的小物块压缩而处于静止状态，且弹簧与物块不栓接，弹簧原长小于光滑平台的长度。在平台的右端有一传送带，AB长为L=12m，与传送带相邻的粗糙水平面BC长为x=4m，物块与传送带及水平面BC间的动摩擦因数均为，在C点右侧有一半径为R的光滑竖直半圆弧与BC平滑连接，在半圆弧的最高点F处有一固定挡板，物块撞上挡板后会以原速率反弹回来。若传送带以的速率顺时针转动，不考虑物块滑上和滑下传送带的机械能损失。当弹簧储存的能量全部释放时，小物块恰能滑到与圆心等高的E点（取g=10m/s2）。

（1）求滑块被弹簧弹出时的速度；

（2）求右侧圆弧的轨道半径R；

（3）若传送带的速度大小可调，欲使小物块与挡板只碰一次，且碰后不脱离轨道，求传送带速度的可调范围。

试题分类