��Ŀ����
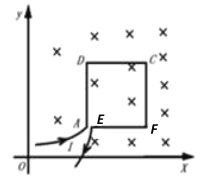
����Ŀ����ͼ��ʾ��ˮƽ��������������ƽ�����㹻���Ĺ⻬������������Ǽ�ľ���L=0.20m��������������֮�����һ��R=0.10���ĵ��衣������OO����OO����ֱ�ڹ�����Ҳ��з�����ֱ���µ���ǿ�ų����Ÿ�Ӧǿ��B=0.50T��һ������m=0.10kg��ֱ������ab��ֱ�ڹ��������������ϡ�ijʱ�̸�ab��v0=2.0m/s��ƽ���ڹ���ij��ٶȽ���ų���ͬʱ�ڸ���ʩ��һ��ˮƽ������ʹ����a=2.0m/s2�ļ��ٶ����ȼ���ֱ���˶�����abʼ��������ֱ������֮�䱣�����ýӴ�����ab����ĵ�����ɺ��ԡ�
(1)����ͨ�������жϣ��ڽ�����ab�����˶��Ĺ����У�������ʩ�ӵ�ˮƽ�����ķ���
(2)�ڽ�����ab�����˶��Ĺ����У�����еĸ�Ӧ����Ϊ���ֵ��ʱ��ˮƽ�����Ĵ�С��
(3)�ӽ�����ab����ų����ٶȼ�Ϊ��Ĺ����У�����R�Ϸ���������Q=0.13J����˹�����ˮƽ�������Ĺ���

���𰸡���1��ʼ������2��0����3����7��10��2J
��������
(1)�����˸ս���ų�ʱ�����еĸ�Ӧ����Ϊ
I0=![]()
![]()
��ʱ����ab���ܵİ�����Ϊ
F��=BI0L=0.5��2��0.2N=0.2N
����ˮƽ������ţ�ٵڶ����ɵã���ab���ܵĺ���Ϊ
F��=ma=0.1��2N=0.2N
����ˮƽ�����ڽ�����ab�������ȼ���ֱ���˶��Ĺ����У�������F�����ϼ�С����ˣ�������ʩ�ӵ�ˮƽ�����ķ���ʼ��ˮƽ����
(2)���˸ս���ų�ʱ��������ٶ�Ϊv0=2.0m/sʱ����ʱ��ab���ܵİ�����Ϊ
F��=BI0L=0.5��2��0.2N=0.2N
����ˮƽ������ţ�ٵڶ����ɵ�
F��+F=ma
ˮƽ�����Ĵ�СΪ
F=ma��F��=0
(3)�ɶ��ܶ�����
W��+WF=0��![]()
���п˷���������������ֵ���ڵ���R�Ϸ���������Q����
��W��=Q
������
WF=Q��![]() =0.13J��
=0.13J��![]() J=��7��10��2J
J=��7��10��2J