题目内容
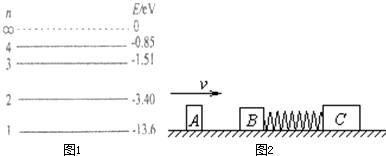
如图1所示,一木块质量为m,沿倾角为θ的斜面下滑,木块与斜面间的动摩擦因数为μ,现用水平外力F推木块,试问F为何值时,木块会保持静止.

?摇可以预见,F的取值应是一个范围.首先以木块为研究对象,当F较小时,如图2所示物体受重力mg、支持力N、沿斜面向上的滑动摩擦力f和水平向右的推力F.物体刚好静止时,应是F的边界值,此时的摩擦力为最大静摩擦力,可近似看成fmax=μN(最大静摩擦力).如图2建立坐标系,由牛顿第二定律列方程:
x轴:mgsinθ-fmax-Fcosθ=0 ①
y轴:N-mgcosθ-Fsinθ=0 ②
fmax=μN ③
解上面三个方程式,得F=(sinθ-μcosθ)mg/(cosθ+μsinθ).
当F从此值开始增加时,静摩擦力方向开始仍然斜向上,但大小会减小.当F增加到Fcosθ= mgsinθ时,即F=mgtan θ时,静摩擦力减小到零.F再增加,静摩擦力的方向改为沿斜面向下,可以根据受力分析图3列出方程:
x轴:mgsinθ+f-Fcosθ=0 ④
y轴:N-mgcosθ-Fsinθ=0 ⑤
f=μN ⑥
随着推力F的增加,静摩擦力增加,F最大值对应斜向下的最大静摩擦力.
依据④⑤⑥三式,解得
F=(sinθ+μcosθ)mg/(cosθ-μsinθ).
要使木块静止在斜面上,推力F的值应为
 mg≤F≤
mg≤F≤ mg.
mg.【试题分析】

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
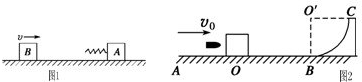
 Ⅰ.某同学在做测定木块与木板间动摩擦因数的实验过程中,测滑动摩擦力时,他设计了两种实验方案.
Ⅰ.某同学在做测定木块与木板间动摩擦因数的实验过程中,测滑动摩擦力时,他设计了两种实验方案.