��Ŀ����
9��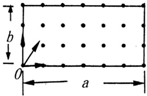 ��ͼ��ʾ����Ϊa��Ϊb�ľ��������ڣ������߽磩�дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱֽ�����⣮0����һ����Դ��ijʱ������Դ��ų�����������ų���ֱ��ƽ�������з������������Ϊm����Ϊq�Ĵ���������ӣ����ӵ��ٶȴ�С��ͬ�������ڴų���������Բ���˶�������ΪT�����ȴӴų��ϱ߽���������Ӿ�����ʱ��Ϊ$\frac{T}{12}$�����Ӵų��зɳ������Ӿ�����ʱ��Ϊ$\frac{T}{4}$����������������֮�������ã�������
��ͼ��ʾ����Ϊa��Ϊb�ľ��������ڣ������߽磩�дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱֽ�����⣮0����һ����Դ��ijʱ������Դ��ų�����������ų���ֱ��ƽ�������з������������Ϊm����Ϊq�Ĵ���������ӣ����ӵ��ٶȴ�С��ͬ�������ڴų���������Բ���˶�������ΪT�����ȴӴų��ϱ߽���������Ӿ�����ʱ��Ϊ$\frac{T}{12}$�����Ӵų��зɳ������Ӿ�����ʱ��Ϊ$\frac{T}{4}$����������������֮�������ã�������| A�� | �����ٶȴ�СΪ$\frac{qBb}{m}$ | |
| B�� | ������Բ���˶��İ뾶Ϊ3b | |
| C�� | a�ij�����$\sqrt{3}$+1��b | |
| D�� | ���Ӵų��зɳ�������һ�����ϱ߽���е�ɳ� |
���� �������ֶ����֪�������ڴų����ܵ������������ķ������ң�������ƫת�����˶����ص����˶������ʱ�䣬�����жϳ�ƫת�ĽǶȣ�Ȼ���ɼ��ι�ϵ������ӵİ뾶�����������ṩ��������������˶����ٶȣ����ݼ��ι�ϵ���жϳ����Ӵų��зɳ������ӵĹ켣���ó�a�ij����Լ����ӷɳ��ų���λ�ã�
��� �⣺A��B���������ֶ����֪�������ڴų����ܵ������������ķ������ң�������ƫת������˶����ص��֪���������ϵķ��ٶ�Խ����Խ����ϱ߽�ɳ�������������ϱ߽�ɳ������ӽ���ų��ķ�������ֱ���ϵģ�
���������ȴӴų��ϱ߽���������Ӿ�����ʱ��Ϊ$\frac{T}{12}$�����ݣ�$\frac{t}{T}=\frac{��}{360��}$��������ƫת�ĽǶȣ�$��=\frac{t}{T}��360=\frac{1}{12}��360=30��$��
������������������˶��Ĺ켣��ͼ1����ͼ�м��ι�ϵ��֪��$r=\frac{b}{sin30��}=2b$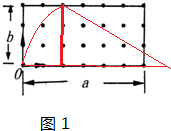
�����ڴų����˶������������ṩ������������$qvB=\frac{m{v}^{2}}{r}$
���ԣ�$v=\frac{qBr}{m}=\frac{2qBb}{m}$����A����B����
C��D�����ӵ�����ķ�����90��ķ�Χ���ڣ���r=2b�����������˶��Ĺ켣���ᳬ�����Բ���˶���ʱ�䲻����������ڣ���$\frac{t}{T}=\frac{��}{360��}$��֪���켣��Բ�Ľ�Խ�����˶���ʱ��Խ������Բ�Ľ�Խ��Ӧ���ҳ�Խ�������������˶����ʱ��Ĺ켣���ҳ�Ҳ��������������ų�������һ���ǴӴų����ұ���������Ӵų��зɳ������Ӿ�����ʱ��Ϊ$\frac{T}{4}$�������˶�����켣��ͼ2��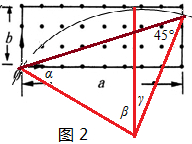
��$sin��=\frac{r-b}{r}=\frac{2b-b}{2b}=\frac{1}{2}$
���ԣ���=30�㣬��=90��-��=60�㣬
�������Ӵų��зɳ������Ӿ�����ʱ��Ϊ$\frac{T}{4}$����ƫת�ǵ���90�㣬��=90��-��=30��
�ɼ��ι�ϵ�ɵã�$a=r•cos��+r•sin��=2b•cos30��+2b•sin30��=��\sqrt{3}+1��b$����C��ȷ��D����
��ѡ��C
���� ���⿼����������ڴų����˶��ļ����ٽ����⣬����Ĺؼ��Ǹ�����Ŀ����������ȷ���������˶��Ĺ켣��Ȼ����˶��Ĺ켣��ȷ���ٽ������ͼ��ι�ϵ��

 ��У����ϵ�д�
��У����ϵ�д�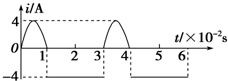
| A�� | 4A | B�� | 2$\sqrt{2}$A | C�� | $\frac{8}{3}$A | D�� | $\frac{2\sqrt{30}}{3}$A |
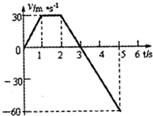 ij��ѧ������ˮƽ�������������Ƶ�һö����������������պ�����ֱ�������˶���v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������
ij��ѧ������ˮƽ�������������Ƶ�һö����������������պ�����ֱ�������˶���v-tͼ����ͼ��ʾ��������˵������ȷ���ǣ�������| A�� | 0��1s�ڻ���������� | B�� | 1��2s�ڻ����ֹ���� | ||
| C�� | 3sĩ����ص������� | D�� | 5sĩ����ص������� |
| A�� | ��Ȼ��������˵��ԭ�Ӻ˻����и��ӽṹ | |
| B�� | һ�������䵽ij�ֽ����ϲ��ܷ������ЧӦ����������Ϊ������Ĺ�ǿ̫С | |
| C�� | ��14 eV�Ĺ������䴦�ڻ�̬����ԭ�ӣ���ʹ����� | |
| D�� | ${\;}_{6}^{14}$C�İ�˥��Ϊ5 730�꣬�����һ�������ź��е�${\;}_{6}^{14}$C����ֻ�л����е�$\frac{1}{8}$������ź����Լ��45840�� | |
| E�� | ������Ԫ�صİ�˥����Ԫ�������������ͻ�ѧ״̬�أ�����һ��ͳ�ƹ��ɣ�ֻ�Դ����ķ�����ԭ�Ӻ˲����� |
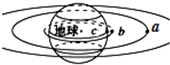 ��ͼ��ʾ��a�ǵ����ͬ�����ǣ�b��λ�ڳ��ƽ���ڵĽ������ǣ�cΪ�������ϵ����壬��֪����뾶ΪR��ͬ�����������ĸ߶�Ϊh��������
��ͼ��ʾ��a�ǵ����ͬ�����ǣ�b��λ�ڳ��ƽ���ڵĽ������ǣ�cΪ�������ϵ����壬��֪����뾶ΪR��ͬ�����������ĸ߶�Ϊh��������| A�� | a��b���ٶȵĴ�С֮��Ϊ��$\frac{R+h}{R}$��2 | |
| B�� | a��c���ٶȵĴ�С֮��Ϊ1+$\frac{h}{R}$ | |
| C�� | a��b��c�ٶȴ�С��ϵΪva��vb��vc | |
| D�� | Ҫ��b����ת�Ƶ�a���ǵĹ��������������Ҫ��b���ǽ������μ��� |
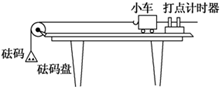 ����ͼ��ʾ��װ��̽�����ٶ��������Ĺ�ϵʱ����������������̵��������䣬��С���Ϸ����룬��MΪС��������������ͣ��ı�M�ظ�ʵ�飬ȷ�����ٶ�a��$\frac{1}{M}$�Ĺ�ϵ������ͼ��ʾ��ͼ���ܱ�ʾ��ͬѧʵ�������� ��������
����ͼ��ʾ��װ��̽�����ٶ��������Ĺ�ϵʱ����������������̵��������䣬��С���Ϸ����룬��MΪС��������������ͣ��ı�M�ظ�ʵ�飬ȷ�����ٶ�a��$\frac{1}{M}$�Ĺ�ϵ������ͼ��ʾ��ͼ���ܱ�ʾ��ͬѧʵ�������� ��������



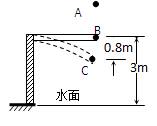 ����ˮ�����У���һ�������ǡ�3m���塱����������̿ɼ�Ϊ���˶�Ա�������壬�پ��������˶����˶�Ա�������ˮƽ��B���2m/s����ֱ���µij��ٶȣ�ֱ�����屻ѹ������͵�C���������彫�˶�Ա��ֱ���ϵ�����ߵ㣬�˶�Ա�����������˶�����ֱ����ˮ�У����˶�Ա��Ϊ�ʵ㣬�˶�Ա����m=50kg��g=10m/s����ߵ�A�������ˮƽ��B����͵�C��ˮ��֮�����ֱ������ͼ��ʾ����
����ˮ�����У���һ�������ǡ�3m���塱����������̿ɼ�Ϊ���˶�Ա�������壬�پ��������˶����˶�Ա�������ˮƽ��B���2m/s����ֱ���µij��ٶȣ�ֱ�����屻ѹ������͵�C���������彫�˶�Ա��ֱ���ϵ�����ߵ㣬�˶�Ա�����������˶�����ֱ����ˮ�У����˶�Ա��Ϊ�ʵ㣬�˶�Ա����m=50kg��g=10m/s����ߵ�A�������ˮƽ��B����͵�C��ˮ��֮�����ֱ������ͼ��ʾ����
 ͼ��a����һ�����ѹ���ĵ�·����ͼ��ͼ��b����ԭ��Ȧ�������ӵĵ�ѹ��ʱ��仯�Ĺ�ϵͼ����֪��ѹ����ʾ��Ϊ20V��������ֵ�������ֵR��Ϊ10������
ͼ��a����һ�����ѹ���ĵ�·����ͼ��ͼ��b����ԭ��Ȧ�������ӵĵ�ѹ��ʱ��仯�Ĺ�ϵͼ����֪��ѹ����ʾ��Ϊ20V��������ֵ�������ֵR��Ϊ10������