题目内容
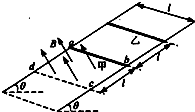
如图所示，电阻不计的足够长光滑平行金属导轨与水平面夹角为θ，导轨间距为l，轨道所在平面的正方形区域如耐内存在着有界匀强磁场，磁感应强度大小为B，方向垂直于导轨平面向上．电阻相同、质量均为m的两根相同金属杆甲和乙放置在导轨上，甲金属杆恰好处在磁场的上边界处，甲、乙相距也为l．在静止释放两金属杆的同时，对甲施加一沿导轨平面且垂直甲金属杆的外力，使甲在沿导轨向下的运动过程中始终以加速度a=gsinθ做匀加速直线运动，金属杆乙剐进入磁场时即做匀速运动．
（1）求金属杆的电阻R；
（2）若从释放金属杆时开始计时，试写出甲金属杆在磁场中所受的外力F随时间t的变化关系式；
（3）若从开始释放两金属杆到金属杆乙刚离开磁场的过程中，金属杆乙中所产生的焦耳热为Q，求外力F在此过程中所做的功．
分析：金属杆由静止做匀加速直线运动，运动l后，进入磁场时即做匀速运动．由平衡条件可求，安培力进而求得电流、电阻，由牛顿第二定律，可求外力，由焦耳定律可求
金属杆乙中所产生的焦耳热，由能量守恒定律可求外力的功．
解答：解：（1）在乙尚未进入磁场中的过程中，甲、乙的加速度相同，设乙刚进入磁场时的速
v
2=2ax 且 a=gsinθ
即 v=
乙刚进入磁场时，对乙由根据平衡条件得
mgsinθ= R=（2）甲在磁场中运动时，由牛顿第二定律可知，外力F大小始终等于安培力火小即：
F= v=（gsinθ）
解得
F=t 方向沿导轨平面并垂直金属杆甲向下
（3）设乙从释放到刚进入磁场过程中做匀加速直线运动所需要的时间为t
1 l=
(gsinθ) t1==设乙从进入磁场过程至刚离开磁场的过程中做匀速直线运动所需要的时间为t2
l=vt2
t2==设乙离开磁场时，甲的速度v′
v′=（gsinθ）（t
1+t2）=
设甲从开始释放至乙离开磁场的过程中的位移为x
x=(gsinθ)(t1+t2)2=l 根据能量转化和守恒定律得：
mgxsinθ+mg?2lsinθ+WF=2Q+mv2+mv′2 W
F=2Q-mglsinθ
答：（1）金属杆的电阻
R=；
（2）甲金属杆在磁场中所受的外力F随时间t的变化关系式
F=t；
（3）外力F在此过程中所做的功 W
F=2Q-mglsinθ
点评：考查了电磁感应定律，闭合电路欧姆定律的综合应用，注意能量守恒的应用．
练习册系列答案
相关题目
如图所示，电阻不计的平行金属导轨MN和OP水平放置．MO间接有阻值为R的电阻．导轨相距为d，有竖直向下的匀强磁场，磁感强度为B．质量为m，长为L的导体棒CD的电阻为r，垂直于导轨放置，并接触良好．用平行于MN的恒力F向右拉动CD棒．CD棒受恒定的摩擦阻力f．已知F＞f，L＞d，求：
如图所示，电阻不计的平行粗糙长金属导轨固定在一绝缘斜面上，两相同的金属棒a、b垂直于导轨放置，且与导轨良好接触，匀强磁场垂直穿过导轨平面．现用一平行于导轨的恒力F作用在a的中点，使其向上运动．在a运动的整个过程中若b始终保持静止，则它所受摩擦力可能（ ）
如图所示，电阻不计的平行金属导轨MN和OP放置在水平面内，MO间接有阻值为R=3Ω的电阻，导轨相距d=1m，其间有竖直向下的匀强磁场，磁感应强度B=0.5T．质量为m=0.1kg，电阻为r=1Ω的导体棒CD垂直于导轨放置，并接触良好．用平行于MN的恒力F=1N向右拉动CD，CD受摩擦阻力f恒为0.5N．求：（1）CD运动的最大速度；（2）当CD达到最大速度后，电阻R消耗的电功率．
（2013?河南模拟）如图所示，电阻不计的平行光滑金属导轨与水平面的夹角为θ，宽度为l，下端与阻值为R的电阻相连．磁感应强度为B的匀强磁场垂直穿过导轨平面，现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动，滑行到最远位置a′b′后又下湍．已知导体棒运动过程中的最大加速度为2gsinθ，g为重力加速度，轨道足够长，则（ ）
（2012?湛江一模）如图所示，电阻不计的光滑平行金属导轨MN和OP水平放置，MO间接有阻值为R的电阻，两导轨相距为L，其间有竖直向下的匀强磁场．质量为m、长度为L、电阻为R0的导体棒CD垂直于导轨放置，并接触良好．在CD的中点处用大小为F平行于MN向右的水平恒力啦CD从静止开始运动s的位移，导体棒CD的速度恰好达到最大速度vm．