题目内容
真空中足够大的两个相互平行的金属板a和b之间的距离为d,两板之间电压Uab按图所示规律变化,其变化周期为T.在t=0时刻,一带电粒子(+q)仅在该电场的作用下,由a板从静止开始向b板运动,并于t=nT(n为自然数)时刻,恰好到达b板.求:
(1)若粒子在t=
时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?
(2)若该粒子在t=
时刻才开始从a板运动,需要经过多长时间才能达到b板.

(1)若粒子在t=
| T |
| 6 |
(2)若该粒子在t=
| T |
| 6 |

分析:带电粒子在两板之间电压Uab按图所示规律变化的电场中受到电场力作用,从而做匀变速运动.当a板从静止开始向b板运动,并于t=nT(n为自然数)时刻,恰好到达b板.则当t=
时刻才开始从a板运动,那么经过同样长的时间,前一段时间是先匀加速后匀减速,后一段时间回头匀加速,所以两段时间内的位移之差即为粒子离开a板的距离.由此可知最后一个周期尚未结束就已碰到b板,则可由运动学公式算出碰b板后的时间,从而再减去这个时间.
| T |
| 6 |
解答:(1)设带电粒子在匀强电场中的加速度为a,前半个周期为加速运动,后半个周期为减速运动,
所以a、b间距离d=2ns=2n
a(
)2①
若粒子在t=
时刻开始从a板运动,该粒子向b 板运动的距离x1=2n
a(
T)2.
在电场力作用下返回a 板的距离x2=2n
a(
)2,
该粒子向b板运动的位移:x=x1-x2=2n
a(
T)2-2n
a(
)2②
所以①÷②得:x=
(2)最后一个周期尚未结束就已经碰到b板,则该粒子除去最后一个周期运动时间t1=(3n-1)T,最后一个周期中,粒子加速了
,当减速的
未完成就已和b板相碰,计算时仍可按粒子向b板运动了(
+
)T的时间,再减去碰b板之后的时间,碰b板之后的时间可由粒子反向回b板的两段距离(即反向加速
及减速的
距离)和粒子过b板直到末速度为零时的匀减速的位移相等而求得,即
2×
a(
)2=
解出t2=
T
故粒子从a到b板的总时间为t=t1+t2
所以t=(3n-1)T+
T-
T.
所以a、b间距离d=2ns=2n
| 1 |
| 2 |
| T |
| 2 |
若粒子在t=
| T |
| 6 |
| 1 |
| 2 |
| 2 |
| 6 |
在电场力作用下返回a 板的距离x2=2n
| 1 |
| 2 |
| T |
| 6 |
该粒子向b板运动的位移:x=x1-x2=2n
| 1 |
| 2 |
| 2 |
| 6 |
| 1 |
| 2 |
| T |
| 6 |
所以①÷②得:x=
| d |
| 3 |
(2)最后一个周期尚未结束就已经碰到b板,则该粒子除去最后一个周期运动时间t1=(3n-1)T,最后一个周期中,粒子加速了
| T |
| 3 |
| T |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| T |
| 6 |
| T |
| 6 |
2×
| 1 |
| 2 |
| T |
| 6 |
| 1 |
| 2 |
解出t2=
| ||
| 6 |
故粒子从a到b板的总时间为t=t1+t2
所以t=(3n-1)T+
| 2 |
| 3 |
| ||
| 6 |
点评:由于粒子不是在电场中一直处于加速或减速,所以导致分析运动较复杂.当然第2个问题也可以假设b板向下移动到最后一个周期末速度为零的位置,这算出整段时间,再去移动距离的时间.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 真空中足够大的两个相互平行的金属板a和b之间的距离为d,两板之间的电压Uab按图所示规律变化,其变化周期为T.在t=0时刻,一带电粒子(+q)仅在该电场的作用下,由a板从静止开始向b板运动,并于t=nT(n为自然数)时刻,恰好到达b板.试求:
真空中足够大的两个相互平行的金属板a和b之间的距离为d,两板之间的电压Uab按图所示规律变化,其变化周期为T.在t=0时刻,一带电粒子(+q)仅在该电场的作用下,由a板从静止开始向b板运动,并于t=nT(n为自然数)时刻,恰好到达b板.试求: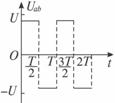

 时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?
时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?
 时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?
时刻才开始从a板运动,那么经过同样长的时间,它将运动到离a板多远的地方?