题目内容
16.关于运动的合成分解,下列说法正确的是( )| A. | 合速度的大小一定比每个分速度的大小都大 | |
| B. | 合运动的方向就是物体实际运动的方向 | |
| C. | 两个匀变速直线运动的合运动一定也是匀变速直线运动 | |
| D. | 两个直线运动的合运动一定也是直线运动 |
分析 当合速度的方向与合加速度的方向在同一条直线上,合运动是直线运动,不在同一条直线上,合运动是曲线运动.
解答 解:A、依据矢量的合成法则,则合速度的大小与每个分速度的大小关系不确定.故A错误.
B、合运动的方向就是物体实际运动的方向.故B正确;
C、两个匀变速直线运动的合运动,当合加速度与合速度共线时,则一定是匀变速直线运动;若两者不共线时,则合运动是匀变速曲线运动.故C错误;
D、两个直线运动的合运动不一定是直线运动.如平抛运动,故D错误;
故选:B.
点评 解决本题的关键掌握判断合运动是直线运动还是曲线运动的方法,关键看合速度的方向与合加速度的方向.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.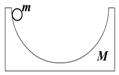 如图所示,质量为M,半径为R的光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
 如图所示,质量为M,半径为R的光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )
如图所示,质量为M,半径为R的光滑圆弧轨道静止于光滑水平面上,质量为m的小球从静止开始自圆弧轨道的左侧最高点滑下,则( )| A. | m能到达圆弧轨道右侧的最高位置与初始位置等高 | |
| B. | m能到达圆弧轨道右侧的最高位置比初始位置低,不会滑出圆弧轨道 | |
| C. | m能到达圆弧轨道右侧的最高位置比初始位置高,将滑出圆弧轨道 | |
| D. | m到达圆弧轨道右侧最高位置时,M将会向左移动一段位移 |
11. 如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=0.4Ω的电阻,导轨所在的空间存在竖直向下的匀强磁场,磁感应强度B=0.1T,导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好.电阻RMN=0.1Ω.设导体棒沿导轨向右匀速运动,速度v=5m/s,导轨的电阻不计,下列说法正确的是( )
如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=0.4Ω的电阻,导轨所在的空间存在竖直向下的匀强磁场,磁感应强度B=0.1T,导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好.电阻RMN=0.1Ω.设导体棒沿导轨向右匀速运动,速度v=5m/s,导轨的电阻不计,下列说法正确的是( )
 如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=0.4Ω的电阻,导轨所在的空间存在竖直向下的匀强磁场,磁感应强度B=0.1T,导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好.电阻RMN=0.1Ω.设导体棒沿导轨向右匀速运动,速度v=5m/s,导轨的电阻不计,下列说法正确的是( )
如图所示,足够长的平行光滑金属导轨水平放置,宽度L=0.4m,一端连接R=0.4Ω的电阻,导轨所在的空间存在竖直向下的匀强磁场,磁感应强度B=0.1T,导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好.电阻RMN=0.1Ω.设导体棒沿导轨向右匀速运动,速度v=5m/s,导轨的电阻不计,下列说法正确的是( )| A. | 导体棒MN相当于电源,N相当于电源的正极 | |
| B. | 电源的电动势为0.2V,感应电流为0.4A | |
| C. | 导体棒所受安培力大小为0.016,方向水平向右 | |
| D. | MN两端的电压为0.2V,电源内部消耗的功率为0.08W |
4. 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
 质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )| A. | A球的速度最大时,角BOA的角平分线在竖直方向 | |
| B. | A球的速度最大时,两小球的重力势能之和最小 | |
| C. | A球的速度最大时,A球在其运动圆周的最低点 | |
| D. | A球的速度最大时,两直角边与竖直方向的夹角为45° |
11.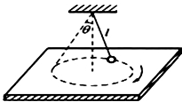 如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
 如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )
如图所示,长为l的绳子下端连着质量为m的小球,上端悬于天花板上,当绳子拉直时,绳子与竖直方向的夹角为60°,此时,小球静止于光滑水平桌面上,重力加速度为g.则( )| A. | 当小球以角速度ω=做圆锥摆运动时,绳子的张力大小等于重力大小 | |
| B. | 当小球以角速度ω=做圆锥摆运动时,桌面对小球的支持力大小等于重力大小 | |
| C. | 当小球以角速度ω=2做圆锥摆运动时,绳子的张力大小等于重力大小的3倍 | |
| D. | 当小球以角速度ω=做圆锥摆运动时,桌面对小球恰好没有支持力的作用 |
8. 如图所示,竖直光滑圆弧形管道MC半径为R,它与水平管道CD恰好相切,与CD处于同一水平面上的A、B两点和C点的连线构成边长为L的等边三角形.D点恰好位于AB的中点,在A、B两点分别固定有电量为q的等量异种电荷.现将质量为m,带电量为+Q的小球(小球直径略小于管径)由圆弧管道最高点M处静止释放,不计+Q电荷对叠加电场的影响及电量损失,取无穷远处为零电势,静电力常量为k,重力加速度为g,则下列说法正确的是( )
如图所示,竖直光滑圆弧形管道MC半径为R,它与水平管道CD恰好相切,与CD处于同一水平面上的A、B两点和C点的连线构成边长为L的等边三角形.D点恰好位于AB的中点,在A、B两点分别固定有电量为q的等量异种电荷.现将质量为m,带电量为+Q的小球(小球直径略小于管径)由圆弧管道最高点M处静止释放,不计+Q电荷对叠加电场的影响及电量损失,取无穷远处为零电势,静电力常量为k,重力加速度为g,则下列说法正确的是( )
 如图所示,竖直光滑圆弧形管道MC半径为R,它与水平管道CD恰好相切,与CD处于同一水平面上的A、B两点和C点的连线构成边长为L的等边三角形.D点恰好位于AB的中点,在A、B两点分别固定有电量为q的等量异种电荷.现将质量为m,带电量为+Q的小球(小球直径略小于管径)由圆弧管道最高点M处静止释放,不计+Q电荷对叠加电场的影响及电量损失,取无穷远处为零电势,静电力常量为k,重力加速度为g,则下列说法正确的是( )
如图所示,竖直光滑圆弧形管道MC半径为R,它与水平管道CD恰好相切,与CD处于同一水平面上的A、B两点和C点的连线构成边长为L的等边三角形.D点恰好位于AB的中点,在A、B两点分别固定有电量为q的等量异种电荷.现将质量为m,带电量为+Q的小球(小球直径略小于管径)由圆弧管道最高点M处静止释放,不计+Q电荷对叠加电场的影响及电量损失,取无穷远处为零电势,静电力常量为k,重力加速度为g,则下列说法正确的是( )| A. | D点的电势为零 | |
| B. | 球在管道中运动时,其机械能守恒 | |
| C. | 球在圆弧管道中运动时速度是先增大后减小 | |
| D. | 球对圆弧形管道最低点C处的压力大小为3mg |

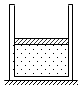 如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求:
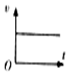
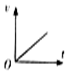
如图所示,内壁光滑、导热良好的汽缸中封闭了一定质量的理想气体,活塞到缸底的距离h=0.5m.已知活塞质量m=2kg,横截面积S=1×10-3m2,环境温度t=0℃且保持不变,外界大气压强p0=1×105Pa,阿伏加德罗常数NA=6×1023mol-1,标准状态下气体的摩尔体积Vmol=22.4L/mol,g=10m/s2.现将汽缸缓慢地转至开口水平,求: 如图是物运动的x-t图象,则选项中与之相对应的v-t图象是( )
如图是物运动的x-t图象,则选项中与之相对应的v-t图象是( )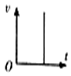

 在“验证机械能守恒定律”的实验中
在“验证机械能守恒定律”的实验中