题目内容
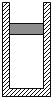
【题目】如图，一上端开口、下端封闭的细长玻璃管，上部有长24cm的水银柱，封有长12cm的空气柱，此时水银面恰好与管口平齐．已知大气压强为p0=76cmHg ， 如果使玻璃管绕底端在竖直平面内缓慢地转动180°，求在开口向下时管中空气柱的长度．封入的气体可视为理想气体，在转动过程中气体温度保持不变，没有发生漏气．
【答案】解答：设玻璃管开口向上时，空气柱的压强为
p1=p0+ρgl1 ①
式中，ρ和g分别表示水银的密度和重力加速度．
玻璃管开口向下时，原来上部的水银有一部分会流出，设此时空气柱长度为x ， 则
p2=p0﹣ρg[（l1+l2）﹣x]②
式中，p2为管内空气柱的压强．由玻意耳定律有
p1l2S=p2xS ③
S为玻璃管的横截面积，由①②③式和题干条件得
x=20 cm
答：在开口向下时管中空气柱的长度为20cm ．
【解析】在玻璃管转动过程中，根据P=P0+hcosθ可知，转动的角度增大，封闭气体压强减小，体积增大，水银溢出，整个过程封闭气体等温变化，根据玻意耳定律列式求解即可．
练习册系列答案
相关题目
