题目内容
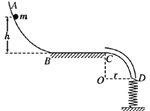
【题目】如图所示，有一倾角为θ=37的粗糙硬杆，其上套一底端固定且劲度系数为k=10N/m的轻弹簀，弹簧自然伸长时上端在Q点，弹簧与杆间摩擦忽略不计。一个质量为m=5kg的小球套在此硬杆上，从P点由静止开始滑下，经过t=2s后，P与弹簧自由端Q相碰，PQ间的距离L=4m，弹簧的弹性势能与其形变量x的关系为
。已知sin37 =0.6，cos37=0.8， 重力加速度g取10m/s.求：
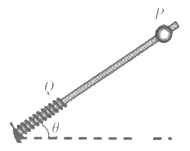
(1)小球与硬杆之间的滑动摩擦因数μ；
(2)小球向下运动过程中速度最大时弹簧的弹性势能。
【答案】（1）0.5；（2）5J；
【解析】试题分析：小球做匀加速直线运动，根据运动学公式和牛顿第二定律即可求出摩擦因数；当小球加速度为零时，速度最大，根据平衡条件求出压缩量，再根据
求出速度最大时弹簧的弹性势能。
（1）小球做匀加速直线运动，则有： 
，
解得： 
。
根据牛顿第二定律得： 
解得： 
（2）当小球加速度为零时，速度最大
即有： 
解得：x=1m
所以弹性势能为： 
练习册系列答案
出彩同步大试卷系列答案
相关题目
