题目内容
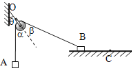
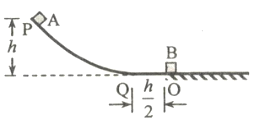
【题目】如图，光滑轨道PQO的水平段QO=
，轨道在O点与水平地面平滑连接。一质量为m的小物块A从高h处由静止开始沿轨道下滑，在O点与质量为4m的静止小物块B发生碰撞。A、B与地面间的动摩擦因数均为
=0.5，重力加速度大小为g。假设A、B间的碰撞为完全弹性碰撞，碰撞时间极短。求
(1)第一次碰撞后瞬间A和B速度的大小；
(2)A、B均停止运动后，二者之间的距离。
【答案】(1)第一次碰撞后瞬间A和B速度的大小分别为
和
(2)A、B均停止运动后它们之间的距离为
【解析】
本题主要考查机械能、匀变速直线运动规律、动量守恒定律、能量守恒定律及其相关的知识点，意在考查考生灵活运用相关知识综合分析问题的的能力。
（1）设A滑到水平轨道的速度为
，则有
①
A与B碰撞时，由动量守恒有
②
由动能不变有
③
联立①②③得：
④
第一次碰撞后瞬间A和B速度的大小分别为和
（2）第一次碰撞后A经过水平段QO所需时间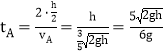
⑤
第一次碰撞后B停下来所需时间
⑥
易知：
故第一次碰撞后B停时，A还没有追上B
设第一次碰撞后B停下来滑动的位移为
，由动能定理得
⑦
解得
⑧
设A第二次碰撞B前的速度为
，由动能定理得
⑨
解得
⑩
，故A与B会发生第二次碰撞
A与B会发生第二次碰撞，由动量守恒有
由动能不变有
解得：
B发生第二次碰撞后，向右滑动的距离为
，由动能定理得
解得
A发生第二次碰撞后，向左滑动的距离为
，由动能定理得
解得
，即A不会再回到光滑轨道PQO的水平段QO上，在O点左边停下
所以A、B均停止运动后它们之间的距离为
=
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
