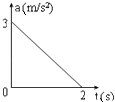
��Ŀ����
����Ŀ����ͼ��ʾ���⻬ˮƽ�����뾶ΪR�Ĺ⻬��ֱ��Բ�����B��ƽ�����ӣ��ڹ�Բ��O��ˮƽ����MN���·��ֲ���ˮƽ���ҵ���ǿ�糡������һ����Ϊm�������Ϊ��q��С���ˮƽ�����A���ɾ�ֹ�ͷţ�С���˶���C���뿪Բ���������MN�ϵ�P�����糡 (P��ǡ����A������Ϸ�����ͼ��С�����Ϊ�ʵ㣬С���˶���C��֮ǰ��������ֲ��䣬����C�������������Ϊ��)����֪AB�����Ϊ2R���������ٶ�Ϊg.�������˶������У���

��1��С���뿪c��ʱ���ٶȴ�С
��2���糡ǿ��E�Ĵ�С
��3����Բ����˶������У�ָ��ʲôλ���ٶ����������С
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
![]()
�������������������1��С���뿪C����ƽ���˶������ݸ߶����ƽ���˶���ʱ�䣬���ˮƽλ�ƺ�ʱ�����С����C����ٶȣ���2����A��C�Ĺ��̣����ö��ܶ���������糡ǿ�ȵĴ�С����3��С�������ٶ���BN�Σ���С���ٶ����ʱ��Բ
�����ߺ���ֱ����ļн�Ϊ![]() �����ݶ��ܶ����������ѧ֪ʶ�������ٶ�.
�����ݶ��ܶ����������ѧ֪ʶ�������ٶ�.
��1��С���뿪C����ƽ���˶�������![]()
���� ![]()
��С����C�����ٶ�![]()
��2����糡ǿ��ΪE��С���A��C�ɶ��ܶ����ã�
![]()
��ã� ![]()
��3����С���˶���Բ��D��ʱ�ٶ����Ϊv����ʱOD����ֱ��OB�н���Ϊ![]()

С���A�˶���D�Ĺ��̣����ݶ��ܶ����ã�
![]()
���� ![]()
������ѧ֪ʶ�ɵã���![]() ʱ�������
ʱ�������
�ɴ˿ɵ�![]()

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�