题目内容
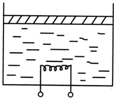如图所示，一圆柱形绝热容器竖直放置，通过绝热活塞封闭着摄氏温度为t1的理想气体，活塞的质量为m，横截面积为S，与容器底部相距h1．现通过电热丝给气体加热一段时间，使其温度上升到t2，若这段时间内气体吸收的热量为Q，已知大气压强为P0，重力加速度为g，求：（1）气体的压强．
（2）这段时间内活塞上升的距离是多少？
（3）这段时间内气体的内能如何变化，变化了多少？
分析：（1）要求封闭气体的压强可以活塞为研究对象，分析受力，根据平衡条件，列式求解．
（2）给气体加热时，封闭气体发生等压变化，可根据盖?吕萨克定律列式求解温度上升到t2时，活塞与容器底部相距的距离h2．即可得到活塞上升的距离．
（3）气体发生等压变化，对活塞的压力大小不变，由公式W=P△V求气体对活塞做功，即可根据热力学第一定律求内能的变化量．
（2）给气体加热时，封闭气体发生等压变化，可根据盖?吕萨克定律列式求解温度上升到t2时，活塞与容器底部相距的距离h2．即可得到活塞上升的距离．
（3）气体发生等压变化，对活塞的压力大小不变，由公式W=P△V求气体对活塞做功，即可根据热力学第一定律求内能的变化量．
解答：解：（1）分析活塞的受力情况，如图所示，根据平衡条件有
mg+P0S=PS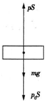
由此得：气体的压强为 P=P0+
（2）设温度上升到t2时，活塞与容器底部相距为h2，因为气体发生等压变化，由盖?吕萨克定律得
=
得：
=
解得，h2=
故活塞上升了△h=h2-h1=
（3）气体对外做功为 W=PS△h=（P0+
）S?△h=（P0S+mg）
根据热力学第一定律△U=W+Q得：△U=Q-W=Q-（P0S+mg）
答：
（1）气体的压强为P0+
．
（2）这段时间内活塞上升的距离是（P0S+mg）
．
（3）这段时间内气体的内能增加，增加了Q-（P0S+mg）
．
mg+P0S=PS
由此得：气体的压强为 P=P0+
| mg |
| S |
（2）设温度上升到t2时，活塞与容器底部相距为h2，因为气体发生等压变化，由盖?吕萨克定律得
| V1 |
| T1 |
| V2 |
| T2 |
得：
| h1S |
| 273+t1 |
| h2S |
| 273+t2 |
解得，h2=
| h1(273+t2) |
| 273+t1 |
故活塞上升了△h=h2-h1=
| h1(t2-t1) |
| 273+t1 |
（3）气体对外做功为 W=PS△h=（P0+
| mg |
| S |
| h1(t2-t1) |
| 273+t1 |
根据热力学第一定律△U=W+Q得：△U=Q-W=Q-（P0S+mg）
| h1(t2-t1) |
| 273+t1 |
答：
（1）气体的压强为P0+
| mg |
| S |
（2）这段时间内活塞上升的距离是（P0S+mg）
| h1(t2-t1) |
| 273+t1 |
（3）这段时间内气体的内能增加，增加了Q-（P0S+mg）
| h1(t2-t1) |
| 273+t1 |
点评：求封闭气体的压强，常常以与气体接触的活塞或水银柱为研究对象，根据力学知识求．对于气体，确定状态发生体积变化是关键．
练习册系列答案
备战中考寒假系列答案
相关题目
如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体，活塞的质量为m，横截面积为S，与容器底部相距h．现通过电热丝缓慢加热气体，当气体吸收热量Q时，活塞上升高度h，此时气体的温度为T1．已知大气压强为p0，重力加速度为g，不计活塞与气缸的摩擦．求：
（1）如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体．活塞的质量为m，横截面积为S，与容器底部相距H．现通过电热丝缓慢加热气体，活塞逐渐上升，活塞与缸壁间摩擦不计．下列说法正确的是_______________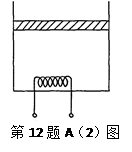
| A．上述过程气体做等压膨胀，温度升高 |
| B．上述过程气体做绝热膨胀，温度升高 |
| C．气体的吸收热量大于它对外做功，内能增加 |
| D．气体吸收的热量等于它对外做功，内能不变 |