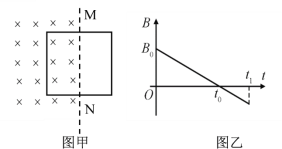��Ŀ����
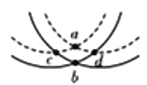
����Ŀ����ͼ��1����ʾ���뾶R=0.45m�Ĺ⻬![]() Բ������̶�����ֱƽ���ڣ�BΪ�������͵㣬B���Ҳ�Ĺ⻬��ˮƽ���Ͻ���B����һ��ֹ��Сƽ�峵��ƽ�峵����M=lkg������l=1m��С�����ϱ�����B��ȸߣ������߶�h=0.2m������m=lkg����飨����Ϊ�ʵ㣩��Բ����ߵ�A�ɾ�ֹ�ͷţ�ȡg=l0m/s2��
Բ������̶�����ֱƽ���ڣ�BΪ�������͵㣬B���Ҳ�Ĺ⻬��ˮƽ���Ͻ���B����һ��ֹ��Сƽ�峵��ƽ�峵����M=lkg������l=1m��С�����ϱ�����B��ȸߣ������߶�h=0.2m������m=lkg����飨����Ϊ�ʵ㣩��Բ����ߵ�A�ɾ�ֹ�ͷţ�ȡg=l0m/s2��
(1)����黬������ϵ�B��ʱ�Թ����ѹ����С��
(2)�������ľ���Ķ�Ħ������0.2��������ƽ�峵�Ҷ˻���ʱƽ�峵���ٶȣ�
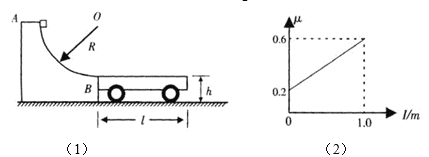
(3)������ƽ�峵�����ϱ�������һ��������ϣ��䶯Ħ���������������������ȱ仯��ͼ��2����ʾ������黬��ƽ�峵ʱ�����ʣ�
���𰸡�(1) 30N (2) 2m/s (3) 1m/s
��������
��1�������A�㵽B��Ĺ����У����е���غ㣬���У�
mgR=![]() mvB2
mvB2
�������ݽ�ã�vB=3m/s����B�㣬��ţ�ٵڶ����ɵã�
N-mg=m![]()
��ã�
N=3mg=3��1��10N=30N
����黬�������B��ʱ�Թ����ѹ��N��=N=30N��������ֱ���¡�
��2����黬��С���������ٶ�Ϊ
a1=��g=2m/s2
�����ȼ����˶���ƽ�峵���ٶ�Ϊ
![]()
�����ȼ����˶�������ʱ��t���룬��
vBt -![]() a1t2-
a1t2-![]() a2t2=l
a2t2=l
�������ݽ�ã�t=0.5s�� (t=1s��ȥ����������黬��ƽ�峵ʱ�ٶ�Ϊ
v=vB-a1t=2m/s
��3�������С���ϻ���ʱ��Ħ��������
![]()
�����忪ʼ����������ƽ�峵�Ĺ��̣��ɶ��ܶ�����
![]()
���v=1m/s��
��(1) 30N (2) 2m/s (3) 1m/s

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�