题目内容
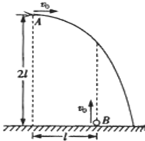如图所示，在距地面2l高空A处以水平初速度v0=| gl |
（1）飞镖从出发到击中气球时所用时间；
（2）击中气球时飞镖的速度大小；
（3）投掷飞镖和放气球两个动作之间的时间间隔应为多少？
分析：（1）飞镖做的是平抛运动，根据水平方向的匀速直线运动可求得运动的时间；
（2）由平抛运动的规律，水平方向匀速直线运动，竖直方向上自由落体可以求得两个方向的分速度的大小，进而可以求得合速度的大小；
（3）分别求出飞镖的运动的时间和气球的运动的时间，即可求得掷飞镖和放气球两个动作之间的时间间隔．
（2）由平抛运动的规律，水平方向匀速直线运动，竖直方向上自由落体可以求得两个方向的分速度的大小，进而可以求得合速度的大小；
（3）分别求出飞镖的运动的时间和气球的运动的时间，即可求得掷飞镖和放气球两个动作之间的时间间隔．
解答：解：（1）飞镖做的是平抛运动，
由水平方向的匀速直线运动可得 l=V0t
所以t=
=
．
所以飞镖运动的时间为
．
（2）飞镖做的是平抛运动，从飞镖飞出到击中气球过程中，
对飞镖来说：l=V0t，Vy=gt，v=
由以上三式联立可得飞镖击中气球时的速度为：v=
．
击中气球时飞镖的速度大小为
．
（3）
飞镖的竖直位移：h=
gt2，
气球上升的位移：H=2l-h，
气球上升的时间：t′=
，
两个动作之间的时间间隔为：△t=t′-t=
，
联立以上各式可求得，气球应比投飞镖早运动的时间为
．
由水平方向的匀速直线运动可得 l=V0t
所以t=
| l |
| v0 |
|
所以飞镖运动的时间为
|
（2）飞镖做的是平抛运动，从飞镖飞出到击中气球过程中，
对飞镖来说：l=V0t，Vy=gt，v=
|
由以上三式联立可得飞镖击中气球时的速度为：v=
| 2gl |
击中气球时飞镖的速度大小为
| 2gl |
（3）
飞镖的竖直位移：h=
| 1 |
| 2 |
气球上升的位移：H=2l-h，
气球上升的时间：t′=
| H |
| V0 |
两个动作之间的时间间隔为：△t=t′-t=
| 1 |
| 2 |
|
联立以上各式可求得，气球应比投飞镖早运动的时间为
| 1 |
| 2 |
|
点评：飞镖做的是平抛运动，气球做的是匀速运动，本题主要是对平抛运动规律的直接考查，掌握住平抛运动的规律就能轻松解决．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图所示，在距地面高为H=15m处，有一不带电的小球A1以v0=10m/s的初速度水平向右抛出，与此同时，在A1的正下方有一带正电滑块A2也在一个水平恒力F的作用下、以相同的初速度v0在绝缘水平地面上向右运动，A1、A2所在空间加有沿水平方向且垂直于纸面向里的足够大的匀强磁场，磁感应强度B=2T．已知A2所带电荷量q=5×10-3C，质量m=0.1kg，F=0.27N，A1、A2均可看作质点，A1着地时恰与A2相撞．若运动中A2的电荷量保持不变，空气阻力不计，重力加速度g取10m/s2，求：
如图所示，在距地面高为H=45m处，有一小球A以初速度v0=10m/s水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度v0同方向滑出，B与地面间的动摩擦因数为μ=0.5，A、B均可看做质点，空气阻力不计，重力加速度g取10m/s2，求：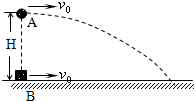
（2009?松江区二模）如图所示，在距地面高为H=45m处，有一小球A以初速度v0=10m/s水平抛出，与此同时，在A的正下方有一物块B也以相同的初速度同方向滑出，B与水平地面间的动摩擦因数为μ=0.4，A、B均可视为质点，空气阻力不计．求A球落地时，A、B相距多远？某同学的解答如下：
高空A处以水平初速度v0＝
投掷飞镖，在与A点水平距离为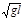
匀速上升，在升空过程中被飞镖击中。飞镖在飞行过程中受到的空气阻力不计，在计算过程中可将飞镖和气球视为质点，已知重力加速度为g。试求：