��Ŀ����
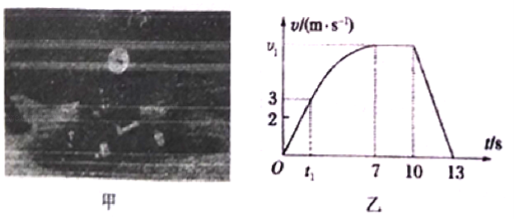
����Ŀ����ͼ����ʾ������M=0.2kg��ƽ�����ˮƽ�����ϣ�����m=0.1kg����飨����Ϊ�ʵ㣩������ƽ���Ϸ�ij��������ϵͳ���ھ�ֹ״̬���ֶ�ƽ��ʩ��һˮƽ���ҵ���������0��1.5s�ڸ�����F��ʱ���ı仯��ϵ��ͼ����ʾ��1.5sĩ��ȥ��������֪���δ��ƽ���ϵ��£���Ϊ���Ħ�����뻬��Ħ������С��ȣ������ľ���Ķ�Ħ��������1=0.2��ƽ��������Ķ�Ħ��������2=0.4��ȡg=10m/s2����:
��1��0��1s������ƽ��ļ��ٶȴ�Сa1��a2��
��2��1sĩ����ƽ����ٶȴ�Сv1��v2�Լ�1.5sĩ����ƽ����ٶȴ�С![]() ��
��![]() ��
��
��3��ƽ�����̳���L��

���𰸡���1��a1=2m/s2��a2=3m/s2����2��v1=2m/s��v2=3m/s��![]() =
=![]() =3m/s����3��L=1.35m��
=3m/s����3��L=1.35m��
��������
��1��![]() �ڣ������ƽ��䡢ƽ��������Ļ���Ħ������С�ֱ�Ϊ��
�ڣ������ƽ��䡢ƽ��������Ļ���Ħ������С�ֱ�Ϊ��
![]()
![]()
�������ƽ���ǡ�û���ʱ������ΪF0
��ţ�ٵڶ�������![]() ����Ϊ
����Ϊ![]() ���������ƽ�巢����Ի�����
���������ƽ�巢����Ի�����
������ƽ����ţ�ٵڶ������У�
![]()
![]()
��ã� ![]()
��2��![]() �ڣ���
�ڣ���![]() ���������ƽ������ȼ���ֱ���˶����У�
���������ƽ������ȼ���ֱ���˶����У�
![]()
��ã�![]()
![]() �ڣ���
�ڣ���![]() ��������ˮƽ���ҵ�����F2=1.4Nǡ����f1+f2ƽ�⣬��ƽ��������ֱ���˶������������ȼ���ֱ���˶�ֱ����ľ���ٶ���ͬ���У�
��������ˮƽ���ҵ�����F2=1.4Nǡ����f1+f2ƽ�⣬��ƽ��������ֱ���˶������������ȼ���ֱ���˶�ֱ����ľ���ٶ���ͬ���У�
![]()
��3����ȥ����![]() ������ƽ��ļ��ٶȴ�С�ֱ�Ϊ��
������ƽ��ļ��ٶȴ�С�ֱ�Ϊ��![]()
����ƽ��ͣ�����õ�ʱ��ֱ�Ϊ��![]()
![]()
�ɻ�����顢ƽ����ٶ�-ʱ��ͼ����ͼ��ʾ���������ٶ�-ʱ��ͼ��������ʾλ������֪�� ![]() �ڣ�������ƽ�������еľ���Ϊ��
�ڣ�������ƽ�������еľ���Ϊ��

![]()
![]() �ڣ�������ƽ�����һ��еľ���Ϊ��
�ڣ�������ƽ�����һ��еľ���Ϊ��![]()
����![]() ���ʣ�
���ʣ�![]() ��
��