题目内容
19.如图甲所示,在水平路段AB上有一质量为2×103kg的汽车,正以20m/s的速度向右匀速运动,汽车前方的水平路段BC较粗糙,汽车通过整个ABC路段的v-t图象如图乙所示(在t=15s处水平虚线与曲线相切),运动过程中汽车发动机的输出功率保持30kW不变,假设汽车在两个路段上受到的阻力(含地面摩擦力和空气阻力等)各自保持不变.求:(1)汽车在AB段及BC段上运动时所受的阻力Ff1和Ff2;
(2)BC路段的长度.

分析 (1)由图象知汽车在AB段匀速直线运动,牵引力等于阻力,而牵引力大小可由瞬时功率表达式求出;由图知,汽车到达B位置将做减速运动,瞬时牵引力大小不变,但阻力大小未知,考虑在t=15s处水平虚线与曲线相切,则汽车又瞬间做匀速直线运动,牵引力的大小与BC段阻力再次相等,有瞬时功率表达式求得此时的牵引力数值即为阻力数值;
(2)BC段汽车做变加速运动,但功率保持不变,需由动能定理求得位移大小.
解答 解:(1)汽车在AB路段做匀速直线运动,根据平衡条件,有:
F1=Ff1,P=F1v1,
解得:Ff1=$\frac{P}{{v}_{1}}$=$\frac{30×1{0}^{3}}{20}$=1500N,
t=15s时汽车处于平衡态,有:F2=Ff2,P=F2v2,
解得:Ff2=$\frac{P}{{v}_{2}}$=$\frac{30×1{0}^{3}}{10}$=3000N;
(2)对于汽车在BC段运动,由动能定理得:Pt-Ff2s=$\frac{1}{2}$mv22-$\frac{1}{2}$mv22,
代入数据解得:s=200m;
答:(1)汽车在AB段及BC段上运动时所受的阻力Ff1和Ff2分别是1500N、3000N;
(2)BC路段的长度为200m.
点评 抓住汽车保持功率不变这一条件,利用瞬时功率表达式求解牵引力,同时注意隐含条件汽车匀速运动时牵引力等于阻力;对于变力做功,汽车非匀变速运动的情况,只能从能量的角度求解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9.2013年6月13日,“神舟十号”飞船与“天宫一号”目标飞行器成功实现自动交会对接,对接轨道所处的空间存在极其稀薄的空气,下面说法正确的是( )
| A. | 为实现对接,两者运行速度的大小都介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 如不加干预.在运行一段时间后,“天宫一号“的动能可能会减少 | |
| C. | 如不加干预,“天宫一号”的轨道高度将缓慢降低 | |
| D. | 航天员在“天宫一号”中不受地球引力作用 |
10.一足球以0.5m/s的速度撞击墙壁,与墙壁作用0.1s后,以0.3m/s的速度反向弹回,以初速度方向为正方向,则足球在与墙壁作用过程中的平均加速度为( )
| A. | -8m/s2 | B. | 8m/s2 | C. | -2m/s2 | D. | 2m/s2 |
7. 如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )
如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )
 如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )
如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )| 位置 | A | B | C |
| 速度(m/s) | 2.0 | 12.0 | 0 |
| 时刻(s) | 0 | 4 | 10 |
| A. | 人与雪橇从A到B的过程中,重力做功为4.2×l03J | |
| B. | 人与雪撬从A到B的过程中,损失的机械能为1.2×104J | |
| C. | 0到4s这段时间内,合外力对人与雪橇做的功为4.2×103J | |
| D. | 0到10s这段时间内,人与雪撬重力做功的平均功率为1.2×103W |
14. 一放在粗糙水平面上的物体在水平外力F和摩擦力作用下运动,1s末撤掉外力F,其v-t图象如图所示,下列表述正确的是( )
一放在粗糙水平面上的物体在水平外力F和摩擦力作用下运动,1s末撤掉外力F,其v-t图象如图所示,下列表述正确的是( )
 一放在粗糙水平面上的物体在水平外力F和摩擦力作用下运动,1s末撤掉外力F,其v-t图象如图所示,下列表述正确的是( )
一放在粗糙水平面上的物体在水平外力F和摩擦力作用下运动,1s末撤掉外力F,其v-t图象如图所示,下列表述正确的是( )| A. | 外力F的大小是摩擦力大小的2倍 | |
| B. | 0~2s内,合外力总是做负功 | |
| C. | 1~2s内,合外力不做功 | |
| D. | 0~3s内,外力F的功等于克服摩擦力的功 |
8.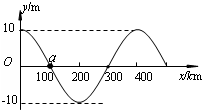 北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )
北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )
 北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )
北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )| A. | 海啸波是电磁波 | |
| B. | 美国夏威夷发生的海啸是日本发生的地震,并将该处的海水传到了美国夏威夷而引起的 | |
| C. | 可以利用地震波传播速度与海啸传播速度的差别造成的时间差进行海啸预警 | |
| D. | 设如图所示海啸波沿+x轴方向传播,图中a点经$\frac{1}{4}$周期时将到达10 m高的波峰处 |
 某学校研究性学习小组想测量木块与木板之间的动摩擦因数.其中一位同学把木板固定在斜面上,他让木块从斜面上端由静止开始匀加速下滑,如图所示,他使用的实验器材仅限于:
某学校研究性学习小组想测量木块与木板之间的动摩擦因数.其中一位同学把木板固定在斜面上,他让木块从斜面上端由静止开始匀加速下滑,如图所示,他使用的实验器材仅限于: 如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=2kg的木块C置于木板B上,水平地面光滑,B、C之间存在摩擦.开始时B、C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s速度弹回.g取10m/s2,求:
如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=2kg的木块C置于木板B上,水平地面光滑,B、C之间存在摩擦.开始时B、C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s速度弹回.g取10m/s2,求: