题目内容
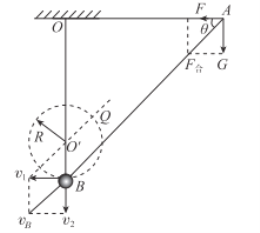
【题目】如图，一质量为m的小球用一长为L的细线悬挂在空中O点，另一端为B点，在O点正下方某处钉一颗钉子O'，整个装置处于某种特殊的空间里，小球始终受到水平向左的力F=mg，现将细线向右水平拉直后从A点无初速度释放，细线碰到钉子后要使小球刚好绕钉子O在竖直平面内做圆周运动，小球的大小忽略不计，求:
(1)小球刚到最低点B点时的速度大小;
(2)O到O的距离.
【答案】(1) 
(2) 
【解析】
(1)初始时刻，
则
θ=45°
摆球在合力F合的作用下沿力的方向做匀加速直线运动，从A点运动到B点，由图可知，△AOB为等腰直角三角形，则摆球从A到B，由动能定理得
，
其中
解得
(2) 在B点处，由于在极短的时间内细线被拉紧，摆球受到细线拉力的作用.法向分量
变为零，切向分量为
在Q点应满足
在等效重力场中，选B为零势能点，根据能量守恒定律得
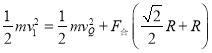
联立方程可解得
所以
练习册系列答案
相关题目
