题目内容
【题目】水平面上有一木板,质量为 M=2kg,板左端放有质量为 m=1kg 的物块(视为 质点),已知物块与木板间动摩擦因数为μ1=0.2,木板与水平面间的动摩擦因数为μ2=0.4。设最大静摩擦力等于滑动摩擦力,取 g=10m/s2。
![]()
(1)现用水平力 F 拉动木板,为使物块与木板一起运动而不相对滑动,求拉力 F 的 大小范围?
(2)若拉动木板的水平力 F=15N,由静止经时间 t1=4s 立即撤去拉力 F,再经t2=1s物块恰好到达板右端,求板长 L=?
【答案】(1)12N<F≤18N(2)1.4m
【解析】
(1)物块与木块一起运动,拉力F必须大于木板与地面之间的最大静摩擦力,当m与M之间的摩擦力达到最大静摩擦力时,拉力F达到最大值;
(2)拉动木板的水平力F=15N,在第(1)问拉力的范围内,整体先做匀加速运动,撤去F后,m向右匀减速,M向右匀减速,当M静止后,m继续向右匀减速到木板右端,求出木板静止前的相对位移和木板静止后物块的位移,即可求出木板的长度;
(1)M与地面之间的最大静摩擦力f1=μ2(M+m)g=0.4×(2+1)×10=12N
当M、m整体一起向右匀加速运动时,当m与M的静摩擦力达到最大静摩擦力时,拉力F最大;
对m:μ1mg=ma①
得a=μ1g=0.2×10m/s2=2m/s2
对整体:Fμ2(M+m)g=(M+m)a②
代入数据:F-12=(2+1)×2
解得:F=18N
所以拉力F大小范围是12N<F≤18N
(2)拉动木板的水平力F=15N,M、m一起匀加速运动
根据牛顿第二定律:![]()
t1=4s时速度v1=at1=1×4m/s=4m/s
撤去F后,物块加速度a1=μ1g=2m/s2
对木板:μ1mgμ2(M+m)g=Ma2,
代入数据:0.2×1012=2 a2
解得:a2=5m/s2
木板向右速度减为0的时间;根据题意t2=1s物块恰好到达板右端![]()
在t1时间内物块的位移:![]()
木板的位移:![]()
物块相对木板的位移△x=x1-x2=2.561.6=0.96m
根据题意撤去力F后,再经t2=1s物块恰好到达板右端
所以木板静止后,木块继续运动0.2s
t1=0.8s时物块的速度v2=v1-a1t1=42×0.8=2.4m/s
![]()
木板长:L=△x+△x′=0.96+0.44=1.4m

【题目】(1)电磁打点计时器和电火花计时器统称为打点计时器。其中电磁打点计时器使用时,电源要求是_____
A.220V直流 B.220V交流 C.4~6V直流 D.4~6V交流
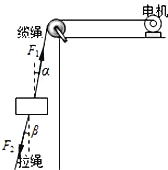
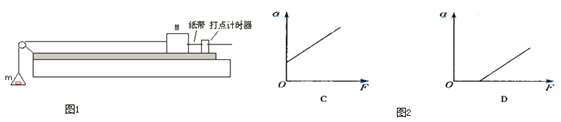
(2)利用下图装置可以做力学中的许多实验,以下说法正确的是_____
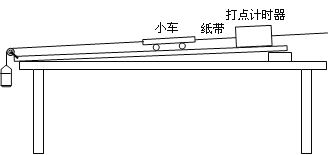
A.用此装置“研究匀变速直线运动”时,必须设法消除小车和滑轨间的摩擦阻力的影响
B.用此装置“研究匀变速直线运动”时,必须调整滑轮高度使连接小车的细线与滑轨平行
C.用此装置“探究加速度a与力F的关系”时,每次改变砂和砂桶总质量之后,需要重新平衡摩擦力
D.用此装置“探究加速度a与力F的关系”时,应使砂和砂桶总质量远小于小车的质量
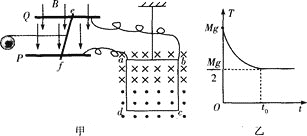
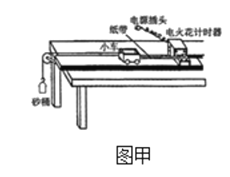
(3)如图甲所示是某同学设计的“探究加速度a与力F、质量m的关系”的实验装置图,实验中认为细绳对小车拉力F等于砂和砂桶总重力,小车运动加速度可由纸带求得。
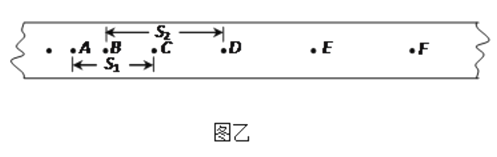
①如图乙所示是该同学在某次实验中利用打点计时器打出的一条纸带,A、B、C、D、E、F是该同学在纸带上选取的六个计数点,相邻计数点间有若干个点未标出,设相邻两个计数点间的时间间隔为T。该同学用刻度尺测出AC间的距离为S1,BD间的距离为S2,则打B点时小车运动的速度vB=__________,小车运动的加速度a=__________。

②某实验小组在实验时保持砂和砂桶总质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的1/m数据如表中所示。根据表中数据,在图丙坐标纸中作出拉力F不变时a与1/m的图象。______________
次数 | 1 | 2 | 3 | 4 | 5 | 6 |
小车加速度a/m·s-2 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 |
小车质量m/kg | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 |
| 3.50 | 3.00 | 2.50 | 2.00 | 1.40 | 1.00 |
③根据图象分析,得到实验结论:_______________________________。