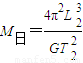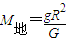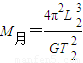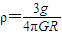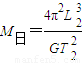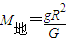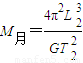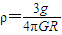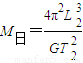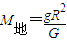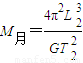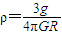题目内容
以表彰伽利略对科学的贡献,2009年被联合国定为“国际天文年”.应用天文望远镜观测到地球中心到月球中心的距离为L1,地球中心到太阳中心的距离为L2,若已知万有引力常量为G,地球表面处的重力加速度为g,地球的半径为R,地球自转的周期为T1,公转周期为T2,则( )
分析:地球绕太阳公转,知道了轨道半径和公转周期利用万有引力提供向心力可求出太阳的质量.根据地球表面的万有引力等于重力,可求出地球的质量,从而求出密度.
解答:解:A、根据G
=M地L2(
)2,得M日=
.故A正确.
B、根据G
=mg,得M地=
.故B正确.
C、月球是环绕天体,不能求出其质量.故C错误.
D、地球的密度ρ=
=
=
.故D正确.
故选ABD.
| M日M地 |
| L22 |
| 2π |
| T2 |
4π2
| ||
G
|
B、根据G
| M地m |
| R2 |
| gR2 |
| G |
C、月球是环绕天体,不能求出其质量.故C错误.
D、地球的密度ρ=
| M地 |
| V |
| ||
|
| 3g |
| 4πGR |
故选ABD.
点评:解决本题的关键掌握万有引力提供向心力:G
=mr(
)2和万有引力等于重力G
=mg.
| Mm |
| r2 |
| 2π |
| T |
| Mm |
| R2 |

练习册系列答案
相关题目