Question

【题目】如图所示，内壁光滑的细圆管道BCD由两个半径R=0.5m的圆弧构成，其D端与水平光滑地面DE相切，E端与一粗糙斜面EF平滑连接，斜面与水平面之间的夹角θ可在0°~90°角范围内变化，一个质量m=0.1kg的小滑块（可视为质点）以的初速度进入管道，已知滑块与斜面之间的动摩擦因数，重力加速度，不计空气阻力

A. 通过B点时，滑块对管道的压力竖直向下

B. 通过D点时，滑块对管道的压力大小为10N

C. θ=60°时，滑块在EF上向上运动的位移最小

D. θ=30°时，滑块沿EF上升的高度比θ=60°时上升的高度大

Answer 1

【答案】BC

【解析】A．设通过B点时，管道对滑块的压力F竖直向下，根据牛顿第二定律：

解得F=4N，根据牛顿第三定律，滑块对管道的压力竖直向上，故A错误；

B．通过D点时，速度为v，管道对滑块的支持力为FN，

根据机械能守恒，

根据牛顿第二定律，

联立解得，F=10N，根据牛顿第三定律，滑块对管道的压力大小为10N，故B正确；

C．设小物块在EF上向上运动的位移为s；

物块整个运动过程只有重力、摩擦力做功,故由动能定理可得：

所以

sinθ+μcosθ=sinθ+cosθ=(sinθ+cosθ)= sin(θ+30)

故当θ=60时,sinθ+μcosθ=最大，位移s最小，故C正确；

D．倾角为60°时的位移最小为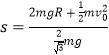=m，滑块沿EF上升的高度为h1=s×sin60°=m=1.688m；倾角为30°时的位移为=2.25m，滑块沿EF上升的高度为h2=2.25×sin30°=1.125m，小于倾角为60°时滑块沿EF上升的高度，故D错误。

故选：BC