题目内容
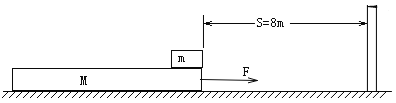
【题目】如图所示,质量为M=2kg足够长的长木板静止在光滑的水平面上,其前端放一质量m=2kg的铁块(可视为质点),铁块与长木板上表面间的动摩擦因数μ=0.2,距离木板的前端s=8m处有一竖直挡板,设铁块、长木板与挡板相碰后均能立即停止运动。现使长木板在水平向右的恒力F作用下由静止开始运动,直至与挡板相碰停止运动。设最大静摩擦力等于滑动摩擦力,g取10m/s2。
(1)若F=6N,求铁块运动的加速度的大小;
(2)若F=12N,求铁块停止运动时的总位移的大小;
(3)为使铁块能运动到挡板处且用时最短,求作用力F的大小及这个最短时间。
【答案】(1)1.5m/s2;(2)8m;(3)8N;2![]() s。
s。
【解析】
(1)M、m保持相对静止的最大加速度满足
![]()
解得:
![]()
M、m一起加速运动所受的最大拉力为
![]()
解得:
![]()
当拉力F=6N<8N,M、m一起加速运动
![]()
解得:
![]()
(2)当F=12N >8N,两者发生相对滑动,m的加速度:
a=μg=2m/s2
M的加速度满足:
F-μmg=Ma2
解得:
a2=4m/s2
M运动到挡板所用的时间为t1,有
![]()
可得:
![]()
该时间内铁块相对地而的位移:
![]()
可得:
x1=4m
此时铁块相对木板向左运动的位移
△x=s-x1
解得:
△x=4m
木板碰到档板后静止,铁块继续向右做匀减速运动,加速度大小为a,假设铁块速度减小到0时位移为x2
![]()
可得:
x2=4m
因x2=△x,说明铁块刚好滑到木板右侧时速度为0
铁块的位移为
x=x1+x2
解得:
x=8m
(3)若要铁块运动到档板处时间最短,则必须保证铁块与木板相对静止并以最大加速度一起运动。最大加速度为a=2m/s2
F=(M+m)a
得:
F=8N
![]()
解得:
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目