题目内容
17.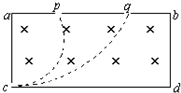 如图所示,在矩形abcd区域内存在着匀强磁场,两带电粒子由静止经同一电场加速后从顶角c处沿cd方向射入磁场,又分别从p、q两处射出,已知cp 连线和cq连线与ac边分别成30°和60°角,不计两粒子的重力.则两粒子在磁场中的运动速率之比(Vp:Vq)为( )
如图所示,在矩形abcd区域内存在着匀强磁场,两带电粒子由静止经同一电场加速后从顶角c处沿cd方向射入磁场,又分别从p、q两处射出,已知cp 连线和cq连线与ac边分别成30°和60°角,不计两粒子的重力.则两粒子在磁场中的运动速率之比(Vp:Vq)为( )| A. | 1:2 | B. | 1:3 | C. | 2:1 | D. | 3:1 |
分析 带电粒子以一定的速度进入匀强磁场,在洛伦兹力的作用下做匀速圆周运动.画出粒子在场中的运动轨迹图,根据几何关系可得两粒子的半径关系,结合动能定理和洛伦兹力提供向心力,列式可求解.
解答 解:由几何关系得,p、q两点射出磁场的粒子做圆周运动的半径分别为: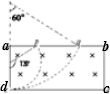
RA=$\frac{2}{3}$ac,RB=2ac,即:RA:RB=1:3,
由动能定理:qU=$\frac{1}{2}$mv2,
洛伦兹力提供向心力:qvB=m$\frac{{v}^{2}}{R}$,
解得:v=$\frac{2U}{BR}$,则:$\frac{{v}_{A}}{{v}_{B}}$=$\frac{{R}_{B}}{{R}_{A}}$=$\frac{3}{1}$;
故选:D.
点评 本题考查了粒子在磁场中的运动,处理带电粒子在磁场中运动的题目解题步骤为:定圆心、画轨迹、求半径;应用动能定理与牛顿第二定律可以解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
 xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )
xOy平面内以O为圆心的圆形区域内有一方向垂直xOy平面的匀强磁场.一个质量为m、电荷量为q的带电粒子由原点O开始运动,初速度为v,方向沿x轴正方向.后来,粒子经过y轴上的P点,如图所示.不计重力的影响,粒子经过P点时的速度方向可能是( )| A. | 箭头a | B. | 箭头b | C. | 箭头c | D. | 箭头d |
8.质量为m的滑块以一定初速度滑上倾角为θ的固定斜面,同时施加一沿斜面向上的恒力F=mgsinθ,已知滑块与斜面间的动摩擦因数μ=tanθ,取出发点为参考点,在滑块从开始运动到最高点的过程中,下列叙述正确的是( )
| A. | 滑块机械能守恒 | |
| B. | 滑块减少的动能大于克服摩擦产生的内能 | |
| C. | 滑块减少的动能等于克服摩擦产生的内能和增加的势能之和 | |
| D. | 滑块减少的动能大于增加的势能 |
5. 竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
 竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )
竖直向上放置的U形管,一端贮有一定质量的理想气体,另一端开口,在温度保持不变的情况下,设想沿CD将右管的上部分截去,则管中封闭的气体体积V和压强p的变化是( )| A. | 体积V和压强p均增大 | B. | 体积V和压强p均减小 | ||
| C. | 体积V增大,压强p减小 | D. | 体积V减小,压强p增大 |
12.一条悬链长7.2m,从悬点处断裂,使其自由下落,不计空气阻力.则整条悬链通过悬链下端正下方12.8m处的一点所需的时间是(g取10m/s2)( )
| A. | 0.3s | B. | 0.4s | C. | 0.7s | D. | 1.2s |
2. 如图所示的电路中,电源电动势为E,内电阻为r.闭合开关S,待电流达到稳定后,电流表示数为I,电压表示数为U,电容器C所带电荷量为Q,将滑动变阻器P的滑动触头从图示位置向a端移动一些,待电流达到稳定后,则与P移动前相比( )
如图所示的电路中,电源电动势为E,内电阻为r.闭合开关S,待电流达到稳定后,电流表示数为I,电压表示数为U,电容器C所带电荷量为Q,将滑动变阻器P的滑动触头从图示位置向a端移动一些,待电流达到稳定后,则与P移动前相比( )
 如图所示的电路中,电源电动势为E,内电阻为r.闭合开关S,待电流达到稳定后,电流表示数为I,电压表示数为U,电容器C所带电荷量为Q,将滑动变阻器P的滑动触头从图示位置向a端移动一些,待电流达到稳定后,则与P移动前相比( )
如图所示的电路中,电源电动势为E,内电阻为r.闭合开关S,待电流达到稳定后,电流表示数为I,电压表示数为U,电容器C所带电荷量为Q,将滑动变阻器P的滑动触头从图示位置向a端移动一些,待电流达到稳定后,则与P移动前相比( )| A. | 电压表示数U变小 | B. | 电流表示数I变小 | ||
| C. | 电容器C所带电荷量Q减小 | D. | 小灯泡L变亮 |
9.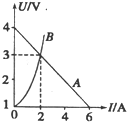 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
 如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )
如图所示,直线A为某电源的U-I图线,曲线B为某小灯泡D1的U-I图线的一部分,用该电源和小灯泡D1组成闭合电路时,灯泡D1恰好能正常发光,则下列说法中正确的是( )| A. | 此电源的电动势为4V | |
| B. | 此电源的内阻为$\frac{2}{3}$Ω | |
| C. | 灯泡D1的额定电压为3V,功率为6W | |
| D. | 把灯泡D1换成一个1Ω的定值电阻,电源的输出功率将变小 |
7.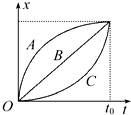 A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
 A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )
A、B、C三质点同时同地沿一直线运动,其x-t图象如图所示,则在0~t0这段时间内,下列说法中正确的是( )| A. | 质点A的位移最大 | B. | 质点C的平均速度最小 | ||
| C. | B质点做匀速直线运动 | D. | 三质点平均速度一定不相等 |