题目内容
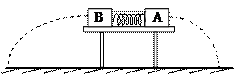
如图所示，在光滑水平面上有两辆车处于静止状态，其上分别站有甲、乙两个小孩，每辆车和小孩的总质量均为M，甲车上的小孩拿着一质量为m的球。现小孩甲将球抛给乙，乙接住后又抛回给甲，如此重复多次，最后球又回到了甲的手中，求甲、乙两车最后的速率之比。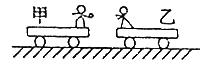
M：（M＋m）
此题若先以甲车及其上的小孩和球为研究对象，应用动量守恒定律列出方程，再以乙车、小孩乙及球为研究对象同样列方程，如此这样分析下去，将非常繁锁。可见，这样选取研究对象显然是不好的。
因为在抛球的过程中，只有两车、两个小孩和球组成的系统之间发生相互作用，因此可以两车、两小孩及球组成的系统为研究对象，以第一次小孩甲抛球时为初态，以最后小孩甲接住球为末态进行研究。因系统在水平方向不受外力，故系统动量守恒。初态系统的总动量为零；末态甲车、小孩及球的总动量为（M＋m）v甲，乙车及其上小孩的总动量为mv乙，设甲车的运动方向为正，则据动量守恒定律便可解得。
解：以两车、两小孩及球组成的系统为研究对象，选最后甲车速度为正方向，设最后甲、乙两车速度分别为v甲、v乙，自始至终系统动量守恒。
对于系统的初、末状态由动量守恒得：
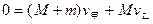
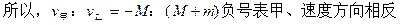
甲、乙速率之比为M：（M＋m）
因为在抛球的过程中，只有两车、两个小孩和球组成的系统之间发生相互作用，因此可以两车、两小孩及球组成的系统为研究对象，以第一次小孩甲抛球时为初态，以最后小孩甲接住球为末态进行研究。因系统在水平方向不受外力，故系统动量守恒。初态系统的总动量为零；末态甲车、小孩及球的总动量为（M＋m）v甲，乙车及其上小孩的总动量为mv乙，设甲车的运动方向为正，则据动量守恒定律便可解得。
解：以两车、两小孩及球组成的系统为研究对象，选最后甲车速度为正方向，设最后甲、乙两车速度分别为v甲、v乙，自始至终系统动量守恒。
对于系统的初、末状态由动量守恒得：
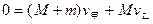
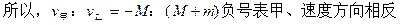
甲、乙速率之比为M：（M＋m）
练习册系列答案
相关题目
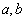两块。若质量较大的
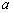块的速度方向仍沿原方向，则：（ ）
的速度方向一定与原速度方向相反 
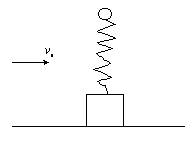
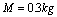的木块（可视为质点），在木块正上方1m处有一固定的悬点O，在悬点O和木块之间用一根长2m、不可伸长的轻绳连接。有一颗质量m=0.1kg的子弹以80m/s的速度射入木块并留在其中，之后木块绕O点在竖直平面内做圆周运动。