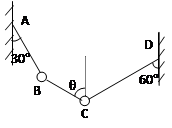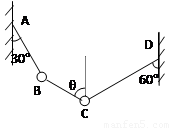题目内容
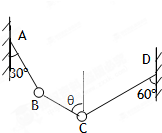如图所示，B、C两个小球均重G，用细线悬挂而静止于A、D两点．求：
（1）AB和CD两根细线的拉力各多大？
（2）细线BC与竖直方向的夹角是多少？
解：（1）对整体分析，运用正交分解得：
FAB=2Gcos30°=1.732G
FCD=2Gcos60°=G
（2）对C球受力分析得：FBCsinθ=Gsin60°
Gcos60°+FBCcosθ=G
所以：θ=60°
答：（1）AB和CD两根细线的拉力各为1.732G、G．
（2）细线BC与竖直方向的夹角是60°．
分析：（1）对整体分析，运用共点力平衡，通过正交分解求出AB、CD两根绳子的拉力．
（2）隔离对C球分析，根据共点力平衡求出细线BC与竖直方向的夹角．
点评：解决本题的关键能够正确地受力分析，运用共点力平衡进行求解，注意整体法和隔离法的运用．
FAB=2Gcos30°=1.732G
FCD=2Gcos60°=G
（2）对C球受力分析得：FBCsinθ=Gsin60°
Gcos60°+FBCcosθ=G
所以：θ=60°
答：（1）AB和CD两根细线的拉力各为1.732G、G．
（2）细线BC与竖直方向的夹角是60°．
分析：（1）对整体分析，运用共点力平衡，通过正交分解求出AB、CD两根绳子的拉力．
（2）隔离对C球分析，根据共点力平衡求出细线BC与竖直方向的夹角．
点评：解决本题的关键能够正确地受力分析，运用共点力平衡进行求解，注意整体法和隔离法的运用．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，B、C两个小球均重G，用细线悬挂而静止于A、D两点．求：
（2011?西乡县模拟）A（选修模块3-4）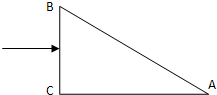
B．（选修模块3-5）
