Question

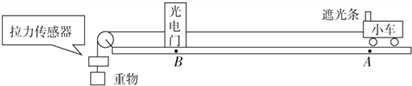
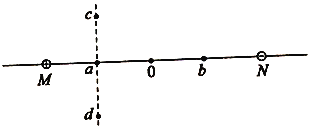
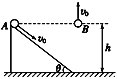
【题目】如图所示，斜面轨道AB与水平面之间的夹角θ=53°，BCD为半径R=5m的圆弧形轨道，在B点，轨道B与与圆弧形轨道BCD相切，整个光滑轨道处于竖直平面内，在A点，一质量为m=1kg的小球由静止滑下，经过B、C点后从D点竖直向上抛出。设以竖直线MDN为分界线，在小球运动到MDN边界以及边界左侧时将受到一个水平向左的恒力F（未知）作用。当小球最后落到与D在同一水平面相距为d=10.8m的S点处，此时速度大小vs=16m/s，已知A点距地面的高度H=10m，B点距地面的高度h=5m.（g取10m/s2），求：

（1）小球经过B点时的速度大小vB=？

（2）小球经过圆弧轨道最低处C点时对轨道的压力

（3）小球从D点抛出后，速度最小时距SD面的高度

Answer 1

【答案】(1)10m/s；(2) 38N；(3)h=1.5m

【解析】（1）对小球，从A到B过程，由动能定理得：mg(Hh)＝mv20
解之小球经过B点时的速度大小v==10m/s
（2）对小球，从B到C过程，由动能定理得：mgR(1cosθ)＝mvc2mv2
在C点，由牛顿第二定律得：Nmg＝m
联立解之得：N=38N
由牛顿第三定律得：小球对轨道的压力为N'=N=38N
（3）对小球，从C到D过程，由动能定理得：mgR＝mvD2mvc2
解之得：vD=2m/s
由D到S: Fd=mvS2-mvD2

F=10N

小球在复合场中受到的合力方向斜向左下45°，大小为mg，把D点的速度分解为垂直于合力和平行于合力方向的分速度，当平行于合力方向的分速度为零时，速度最小

vDcos450＝at
a＝g
竖直方向：x=vDt-gt2
解之得：x=1.5m