题目内容
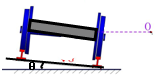
铁路在弯道处的内外轨道高低是不同的．己知内外轨道对水平面倾角为θ，如图所示，弯道处的轨道圆弧半径为尺，若质量为m的火车转弯 时的速度小于| Rgtanθ |
分析：火车以轨道的速度转弯时，其所受的重力和支持力的合力提供向心力，先平行四边形定则求出合力，再根据根据合力等于向心力求出转弯速度，当转弯的实际速度大于或小于轨道速度时，火车所受的重力和支持力的合力不足以提供向心力或大于所需要的向心力，火车有离心趋势或向心趋势，故其轮缘会挤压车轮．
解答：解：火车以某一速度v通过某弯道时，内、外轨道均不受侧压力作用，其所受的重力和支持力的合力提供向心力
由图可以得出
F合=mgtanθ（θ为轨道平面与水平面的夹角）
合力等于向心力，故
mgtanθ=m
，解得v=
．
当速度小于
，重力和支持力的合力大于向心力，对内轨道有挤压．内轨道对火车有斜向上的弹力，则铁轨对火车的支持力小于
．故A正确，B、C、D错误．
故选A．
由图可以得出
F合=mgtanθ（θ为轨道平面与水平面的夹角）
合力等于向心力，故
mgtanθ=m
| v2 |
| R |
| gRtanθ |
当速度小于
| Rgtanθ |
| mg |
| cosθ |
故选A．
点评：本题关键抓住火车所受重力和支持力的合力恰好提供向心力的临界情况，计算出临界速度，然后根据离心运动和向心运动的条件进行分析．
练习册系列答案
相关题目
铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，弯道处的圆弧半径为R，若质量为m的火车以速度v通过某弯道时，内、外轨道均不受侧压力作用，下面分析正确的是（ ）
如图所示，铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，弯道处的圆弧半径为R，质量为m的火车转弯下列说法正确的是（ ）
铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，如图所示．弯道处的圆弧半径为R，若质量为m的火车以v=
铁路在弯道处的内外轨道高低是不同的，其倾角为θ，弯道半径为r，若质量为m的火车转弯时速度V＜v0=| grtanθ |
| A、内轨对内测车轮轮缘有挤压 | ||
| B、外轨对外测车轮轮缘有挤压 | ||
C、铁轨对火车的支持力等于
| ||
D、铁轨对火车的支持力小于
|