题目内容
铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，如图所示弯道处的圆弧半径为R，若质量为m的火车转弯时速度小于| Rgtanθ |
分析：火车在弯道处拐弯时火车的重力和轨道对火车的支持力的合力做为转弯需要的向心力，当合力恰好等于需要的向心力时，火车对内外轨道都没有力的作用，速度增加，就要对外轨挤压，速度减小就要对内轨挤压．
解答：解：A、火车的重力和轨道对火车的支持力的合力恰好等于需要的向心力时，此时火车的速度正好是
，当火车转弯的速度小于
，需要的向心力减小，而重力与支持力的合力不变，所以合力大于了需要的向心力，内轨就要对火车产生一个向外的力来抵消多余的力，所以此时内轨对内侧车轮轮缘有挤压．故A错误，B正确．
C、当内外轨没有挤压力时，受重力和支持力，N=
，由于内轨对火车的作用力沿着轨道平面，可以把这个力分解为水平和竖直向上两个分力，由于竖直向上的分力的作用，使支持力变小．故C、D错误．
故选B．
| Rgtanθ |
| Rgtanθ |
C、当内外轨没有挤压力时，受重力和支持力，N=
| mg |
| cosθ |
故选B．
点评：火车转弯主要是分析清楚向心力的来源，再根据速度的变化，可以知道对内轨还是对外轨由作用力．
练习册系列答案
相关题目
铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，弯道处的圆弧半径为R，若质量为m的火车以速度v通过某弯道时，内、外轨道均不受侧压力作用，下面分析正确的是（ ）
如图所示，铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，弯道处的圆弧半径为R，质量为m的火车转弯下列说法正确的是（ ）
铁路在弯道处的内外轨道高低是不同的，已知内外轨道对水平面倾角为θ，如图所示．弯道处的圆弧半径为R，若质量为m的火车以v=
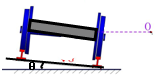铁路在弯道处的内外轨道高低是不同的，其倾角为θ，弯道半径为r，若质量为m的火车转弯时速度V＜v0=| grtanθ |
| A、内轨对内测车轮轮缘有挤压 | ||
| B、外轨对外测车轮轮缘有挤压 | ||
C、铁轨对火车的支持力等于
| ||
D、铁轨对火车的支持力小于
|