Question

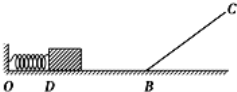
【题目】如图所示，一个轻弹簧水平放置，左端固定在A点，右端与一质量为m1=1kg的物块P接触，但不拴接。AB是水平轨道，B端与半径R=0.8m的竖直光滑半圆轨道BCD底部相切，D是半圆轨道的最高点。另一质量为m2=1kg的物块Q静止于B点。用外力缓慢向左推动物块P，将弹簧压缩（弹簧处于弹性限度内），使物块P静止于距B端L=2m处。现撤去外力，物块P被弹簧弹出后与物块Q发生正碰，碰撞前物块P已经与弹簧分开，且碰撞时间极短，碰撞后两物块粘到一起，并恰好能沿半圆轨道运动到D点。物块P与AB间的动摩擦因数μ=0.5，物块P、Q均可视为质点（g=10m/s2）。求：

（1）与物块Q发生碰撞前瞬间物块P的速度大小；

（2）释放物块P时，弹簧的弹性势能EP。

Answer 1

【答案】（1）4m/s （2）90J

【解析】（1）设与小物块Q发生碰撞前小物块P的速度大小为v0，碰后二者速度大小为v1，在D点速度大小为v2，

在D点：

从B—D过程，由动能定理得：

得：

对P、Q碰撞前后，由动量守恒定律得：

得：

（2）从释放点至B点，对小物块P由动能定理得：

解得：W=EP=90J