题目内容
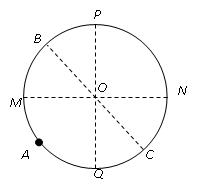
在xOy平面内,直线OP与y轴的夹角α=45°。第一、第二象限内存在方向分别为竖直向下和水平向右的匀强电场,电场强度大小均为E=1.0×105 N/C;在x轴下方有垂直于纸面向外的匀强磁场,磁感应强度B=0.1T,如图所示。现有一带正电的粒子从直线OP上某点A(-L, L)处静止释放。设粒子的比荷 =4.0×107 C/kg,粒子重力不计。求:
=4.0×107 C/kg,粒子重力不计。求:

(1)若L="2" cm,粒子进入磁场时与x轴交点的横坐标及粒子速度的大小和方向;
(2)如果在直线OP上各点释放许多个上述带电粒子(粒子间的相互作用力不计),试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。
 =4.0×107 C/kg,粒子重力不计。求:
=4.0×107 C/kg,粒子重力不计。求: 
(1)若L="2" cm,粒子进入磁场时与x轴交点的横坐标及粒子速度的大小和方向;
(2)如果在直线OP上各点释放许多个上述带电粒子(粒子间的相互作用力不计),试证明各带电粒子进入磁场后做圆周运动的圆心点的集合为一抛物线。
(1)粒子进入磁场时的速度为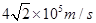 与x轴正方向成45°角斜向下;(2)证明见下
与x轴正方向成45°角斜向下;(2)证明见下
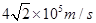 与x轴正方向成45°角斜向下;(2)证明见下
与x轴正方向成45°角斜向下;(2)证明见下试题分析: (1)粒子在第二象限匀加速直线的过程:
 得 v1=4×105 m/s
得 v1=4×105 m/s粒子在第一象限做类平抛运动:

x=v1t
得x="2L=0.04" m ;vx=v1=4×105 m/s;vy=at=4×105 m/s
设粒子进入磁场时速度方向与x轴正方向的夹角为θ,
 则θ=45°
则θ=45°粒子进入磁场时的速度为
 与x轴正方向成45°角斜向下.
与x轴正方向成45°角斜向下.(2)L取任意值时,均有:x0="2L," θ=45°,

粒子在磁场中做匀速圆周运动时,

 代入数据得: R=
代入数据得: R=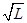
所以圆心的坐标为:
 ,
,
R=
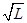 代入并消去L,得
代入并消去L,得x=4y2+y 此方程为一抛物线方程.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 的圆将
的圆将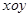 平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于
平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于 的位置。一束质量为
的位置。一束质量为 、电荷量为q、速度为
、电荷量为q、速度为 的带正电粒子从坐标为(
的带正电粒子从坐标为( ,0)的A点沿x轴正方向射入区域Ⅰ,粒子全部垂直打在荧光屏上坐标为(0,-2R)的
,0)的A点沿x轴正方向射入区域Ⅰ,粒子全部垂直打在荧光屏上坐标为(0,-2R)的 点。若区域Ⅱ中加上平行于x轴的匀强电场,从A点沿x轴正方向以速度2
点。若区域Ⅱ中加上平行于x轴的匀强电场,从A点沿x轴正方向以速度2


 试推导出电子比荷
试推导出电子比荷 的表达式;
的表达式;
 ,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为
,0),在y轴与直线MN之间的区域内,存在垂直于xOy平面向外、磁感应强度为B的匀强磁场。在直角坐标系xOy的第Ⅳ象限区域内存在沿y轴,正方向、大小为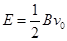 的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0
的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q,电子束以相同的速度v0从y轴上0 y
y ;
;
 .现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求:
.现将一质量为m、带电量为-q(q>0)的小环套在PQ杆上,小环所受的电场力大小为其重力的3倍.(重力加速度为g).求: