题目内容
设在地面上方的真空室内存在匀强电场和匀强磁场.已知电场强度和磁感应强度的方向是相同的,电场强度的大小E=4.0伏/米,磁感应强度的大小B=0.15特.今有一个带负电的质点以v=20米/秒的速度在此区域内沿垂直场强方向做匀速直线运动,求此带电质点的电量与质量之比| q | m |
分析:带电质点受到重力、洛伦兹力电场力,做匀速直线运动时,三个力的合力为零,此三个力在同一竖直平面内,作出受力示意图,根据平衡条件求解.
解答:解:根据带电质点做匀速直线运动的条件,得知此带电质点所受的重力、电场力和洛仑兹力的合力必定为零.由此推知此三个力在同一竖直平面内,如右图所示,质点的速度垂直纸面向外.
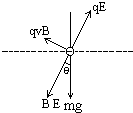 解法一:由合力为零的条件,可得:
解法一:由合力为零的条件,可得:
mg=q
…①
求得带电质点的电量与质量之比
=
…②
代入数据得:
=
C/kg=1.96C/kg…③
因质点带负电,电场方向与电场力方向相反,因而磁场方向也与电场力方向相反.设磁场方向与重力方向之间夹角为θ,则有
qEsinθ=qvBcosθ,
解得:tgθ=
=
=0.75,θ=arctg0.75…④
即磁场是沿着与重力方向夹角θ=arctg0.75,且斜向下方的一切方向.
解法二:因质点带负电,电场方向与电场力方向相反,因而磁砀方向也与电场力方向相反.设磁场方向与重力方向间夹角为θ,由合力为零的条件,可得:
qEsinθ=qvBcosθ…①
qEcosθ+qvBsinθ=mg…②
解得:
=
…③
代入数据得:
=1.96C/kg…④
tgθ=
=
=0.75,θ=arctg0.75…⑤
即磁场是沿着与重力方向成夹角θ=arctg0.75,且斜向下方的一切方向.
答:此带电质点的电量与质量之比
为1.96C/kg,磁场是沿着与重力方向成夹角θ=arctg0.75,且斜向下方的一切方向.
 解法一:由合力为零的条件,可得:
解法一:由合力为零的条件,可得:mg=q
| (vB)2+E2 |
求得带电质点的电量与质量之比
| q |
| m |
| g | ||
|
代入数据得:
| q |
| m |
| 9.80 | ||
|
因质点带负电,电场方向与电场力方向相反,因而磁场方向也与电场力方向相反.设磁场方向与重力方向之间夹角为θ,则有
qEsinθ=qvBcosθ,
解得:tgθ=
| vB |
| E |
| 20×0.15 |
| 4 |
即磁场是沿着与重力方向夹角θ=arctg0.75,且斜向下方的一切方向.
解法二:因质点带负电,电场方向与电场力方向相反,因而磁砀方向也与电场力方向相反.设磁场方向与重力方向间夹角为θ,由合力为零的条件,可得:
qEsinθ=qvBcosθ…①
qEcosθ+qvBsinθ=mg…②
解得:
| q |
| m |
| g | ||
|
代入数据得:
| q |
| m |
tgθ=
| vB |
| E |
| 20×0.15 |
| 4 |
即磁场是沿着与重力方向成夹角θ=arctg0.75,且斜向下方的一切方向.
答:此带电质点的电量与质量之比
| q |
| m |
点评:本题是带电质点在复合场中运动的问题,正确分析受力是关键,要注意磁场方向不是唯一的,而是分布在立体空间,要有空间想象能力,不能漏解.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
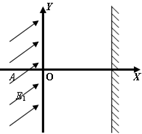 如图,设在地面上方的真空室内,建立平面直角坐标系,在x<0的空间内有倾斜方向的匀强电场,电场强度为E1,在x=0.2m处有一与X轴垂直的荧光屏.一质量为m=4×10-7kg,带电量q=1×10-5C的带电粒子(重力不能忽略)从坐标为(-
如图,设在地面上方的真空室内,建立平面直角坐标系,在x<0的空间内有倾斜方向的匀强电场,电场强度为E1,在x=0.2m处有一与X轴垂直的荧光屏.一质量为m=4×10-7kg,带电量q=1×10-5C的带电粒子(重力不能忽略)从坐标为(-